Kalman's conjecture

Kalman's conjecture or Kalman problem is a disproved conjecture on absolute stability of nonlinear control system with one scalar nonlinearity, which belongs to the sector of linear stability. Kalman's conjecture is a strengthening of Aizerman's conjecture and is a special case of Markus–Yamabe conjecture. This conjecture was proven false but led to the (valid) sufficient criteria on absolute stability.

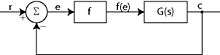
Fig. 1. Block scheme of control system. G(s) – linear transfer function, f(e) – single-valued, continuous, differentiable function

Mathematical statement of Kalman's conjecture (Kalman problem)

In 1957 R. E. Kalman in his paper [1] stated the following:

If f(e) in Fig. 1 is replaced by constants K corresponding to all possible values of f'(e), and it is found that the closed-loop system is stable for all such K, then it intuitively clear that the system must be monostable; i.e., all transient solutions will converge to a unique, stable critical point.

Kalman's statement can be reformulated in the following conjecture:[2]

Consider a system with one scalar nonlinearity

where P is a constant n×n matrix, q, r are constant n-dimensional vectors, ∗ is an operation of transposition, f(e) is scalar function, and f(0) = 0. Suppose, f(e) is a differentiable function and the following condition

is valid. Then Kalman's conjecture is that the system is stable in the large (i.e. a unique stationary point is a global attractor) if all linear systems with f(e) = ke, k ∈ (k1, k2) are asymptotically stable.

In Aizerman's conjecture in place of the condition on the derivative of nonlinearity it is required that the nonlinearity itself belongs to the linear sector.

Kalman's conjecture is true for n ≤ 3 and for n > 3 there are effective methods for construction of counterexamples:[3][4] the nonlinearity derivative belongs to the sector of linear stability, and a unique stable equilibrium coexists with a stable periodic solution (hidden oscillation).

In discrete-time, the Kalman conjecture is only true for n=1, counterexamples for n ≥ 2 can be constructed.[5][6]

gollark: I wouldn't really go above about five or six objects on a flag.
gollark: napaJ
gollark: Maybe put a pentagon around the circle to represent the orbiting bodies instead.
gollark: ...
gollark: And another one (again, doesn't really work as the only reason, but it might be an extra spacey activity): really well-distributed backups of data.

References
  1. Kalman R.E. (1957). "Physical and Mathematical mechanisms of instability in nonlinear automatic control systems". Transactions of ASME. 79 (3): 553–566.
  2. Leonov G.A.; Kuznetsov N.V. (2011). "Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems" (PDF). Doklady Mathematics. 84 (1): 475–481. doi:10.1134/S1064562411040120.
  3. Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. (2011). "Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits" (PDF). Journal of Computer and Systems Sciences International. 50 (5): 511–543. doi:10.1134/S106423071104006X.
  4. Leonov G.A.; Kuznetsov N.V. (2013). "Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits". International Journal of Bifurcation and Chaos. 23 (1): 1330002–219. Bibcode:2013IJBC...2330002L. doi:10.1142/S0218127413300024.
  5. Carrasco J.; Heath W. P.; de la Sen M. (2015). "Second-order counterexample to the Kalman conjecture in discrete-time". 2015 European Control Conference. doi:10.1109/ECC.2015.7330669.
  6. Heath W. P.; Carrasco J; de la Sen M. (2015). "Second-order counterexamples to the discrete-time Kalman conjecture". Automatica. 60: 140–144. doi:10.1016/j.automatica.2015.07.005.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.