k-medoids

The k-medoids or partitioning around medoids (PAM) algorithm is a clustering algorithm reminiscent of the k-means algorithm. Both the k-means and k-medoids algorithms are partitional (breaking the dataset up into groups) and both attempt to minimize the distance between points labeled to be in a cluster and a point designated as the center of that cluster. In contrast to the k-means algorithm, k-medoids chooses data points as centers (medoids or exemplars) and can be used with arbitrary distances, while in k-means the centre of a cluster is not necessarily one of the input data points (it is the average between the points in the cluster). The PAM method was proposed in 1987[1] for the work with ${\displaystyle l_{1}}$ norm and other distances.

k-medoid is a classical partitioning technique of clustering, which clusters the data set of n objects into k clusters, with the number k of clusters assumed known a priori (which implies that the programmer must specify k before the execution of the algorithm). The "goodness" of the given value of k can be assessed with methods such as the silhouette method.

It is more robust to noise and outliers as compared to k-means because it minimizes a sum of pairwise dissimilarities instead of a sum of squared Euclidean distances. (This statement is not correct if the dissimilarity is based on L2 norm; it is therefore misleading. Robustness comes not from not using means, but from using non L-2 metrics such as L-1 or cosine).

A medoid can be defined as the object of a cluster whose average dissimilarity to all the objects in the cluster is minimal, that is, it is a most centrally located point in the cluster.

Algorithms

PAM choosing initial medoids, then iterating to convergence for k=3 clusters, visualized with ELKI.

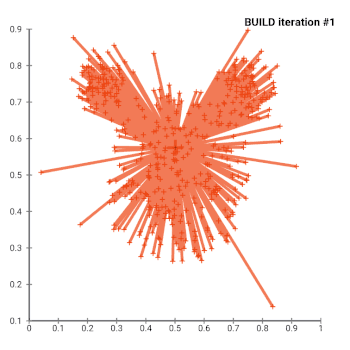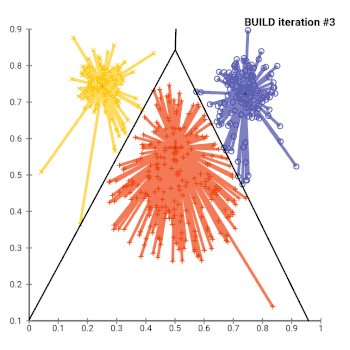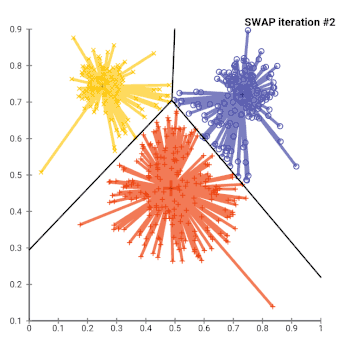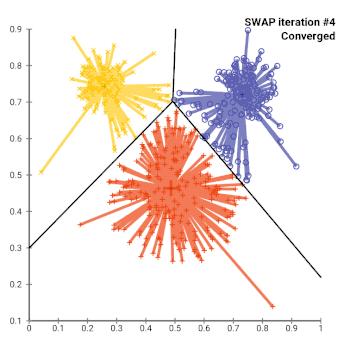
The most common realisation of k-medoid clustering is the partitioning around medoids (PAM) algorithm. PAM uses a greedy search which may not find the optimum solution, but it is faster than exhaustive search. It works as follows:

1. Initialize: greedily select k of the n data points as the medoids to minimize the cost
2. Associate each data point to the closest medoid.
3. While the cost of the configuration decreases:
   1. For each medoid m, and for each non-medoid data point o:
      1. Consider the swap of m and o, and compute the cost change
      2. If the cost change is the current best, remember this m and o combination
   2. Perform the best swap of ${\displaystyle m_{\text{best}}}$ and ${\displaystyle o_{\text{best}}}$, if it decreases the cost function. Otherwise, the algorithm terminates.

The runtime complexity of the original PAM algorithm per iteration of (3) is ${\displaystyle O(k(n-k)^{2})}$, by only computing the change in cost. A naive implementation recomputing the entire cost function every time will be in ${\displaystyle O(n^{2}k^{2})}$. This runtime can be further reduced to ${\displaystyle O(n^{2})}$, by splitting the cost change into three parts such that computations can be shared or avoided.[2]

Algorithms other than PAM have also been suggested in the literature, including the following Voronoi iteration method:[3][4][5]

1. Select initial medoids randomly
2. Iterate while the cost decreases:
   1. In each cluster, make the point that minimizes the sum of distances within the cluster the medoid
   2. Reassign each point to the cluster defined by the closest medoid determined in the previous step.

However, k-means-style Voronoi iteration finds worse results, as it does not allow reassigning points to other clusters while changing means, and thus only explores a smaller search space.[2][6]

The approximate algorithms CLARA and CLARANS trade optimality for runtime. CLARA applies PAM on multiple subsamples, keeping the best result. CLARANS works on the entire data set, but only explores a subset of the possible swaps of medoids and non-medoids using sampling.

Software

• ELKI includes several k-medoid variants, including a Voronoi-iteration k-medoids, the original PAM algorithm, Reynolds' improvements, and the O(n²) FastPAM algorithm, CLARA, CLARANS, FastCLARA and FastCLARANS.
• Julia contains a k-medoid implementation of the k-means style algorithm (faster, but much worse result quality) in the JuliaStats/Clustering.jl package.
• KNIME includes a k-medoid implementation supporting a variety of efficient matrix distance measures, as well as a number of native (and integrated third-party) k-means implementations
• R contains PAM in the "cluster" package, including some of the FastPAM improvements via the pamonce=5 option.
• RapidMiner has an operator named KMedoids, but it does not implement the KMedoids algorithm correctly. Instead, it is a k-means variant, that substitutes the mean with the closest data point (which is not the medoid).
• MATLAB implements PAM, CLARA, and two other algorithms to solve the k-medoid clustering problem.

References

1. Kaufman, L. and Rousseeuw, P.J. (1987), Clustering by means of Medoids, in Statistical Data Analysis Based on the ${\displaystyle L_{1}}$–Norm and Related Methods, edited by Y. Dodge, North-Holland, 405–416.
2. Schubert, Erich; Rousseeuw, Peter J. (2019), Amato, Giuseppe; Gennaro, Claudio; Oria, Vincent; Radovanović, Miloš (eds.), "Faster k-Medoids Clustering: Improving the PAM, CLARA, and CLARANS Algorithms", Similarity Search and Applications, Springer International Publishing, 11807, pp. 171–187, arXiv:1810.05691, doi:10.1007/978-3-030-32047-8_16, ISBN 9783030320461
3. Maranzana, F. E. (1963). "On the location of supply points to minimize transportation costs". IBM Systems Journal. 2 (2): 129–135. doi:10.1147/sj.22.0129.
4. T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning, Springer (2001), 468–469.
5. Park, Hae-Sang; Jun, Chi-Hyuck (2009). "A simple and fast algorithm for K-medoids clustering". Expert Systems with Applications. 36 (2): 3336–3341. doi:10.1016/j.eswa.2008.01.039.
6. Teitz, Michael B.; Bart, Polly (1968-10-01). "Heuristic Methods for Estimating the Generalized Vertex Median of a Weighted Graph". Operations Research. 16 (5): 955–961. doi:10.1287/opre.16.5.955. ISSN 0030-364X.