Jordan's inequality

In mathematics, Jordan's inequality, named after Camille Jordan, states that[1]

{\frac {2}{\pi }}x\leq \sin(x)\leq x{\text{ for }}x\in \left[0,{\frac {\pi }{2}}\right].

{\frac {2}{\pi }}x\leq \sin(x)\leq x{\text{ for }}x\in \left[0,{\frac {\pi }{2}}\right]

unit circle with angle x and a second circle with radius

|EG|=\sin(x)

around E.

{\begin{aligned}&|DE|\leq |{\widehat {DC}}|\leq |{\widehat {DG}}|\\\Leftrightarrow &\sin(x)\leq x\leq {\tfrac {\pi }{2}}\sin(x)\\\Rightarrow &{\tfrac {2}{\pi }}x\leq \sin(x)\leq x\end{aligned}}

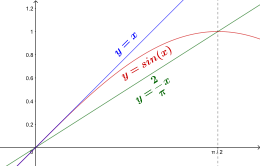
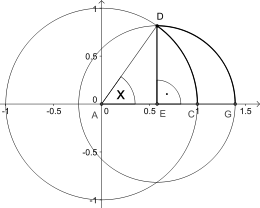
It can be proven through the geometry of circles (see drawing).[2]

Notes

Weisstein, Eric W. "Jordan's inequality". MathWorld.
Nach Feng Yuefeng, Proof without words: Jordan`s inequality, Mathematics Magazine, volume 69, no. 2, 1996, p. 126

Further reading

Serge Colombo: Holomorphic Functions of One Variable. Taylor & Francis 1983, ISBN 0677059507, p. 167-168 (online copy)
Da-Wei Niu, Jian Cao, Feng Qi: Generealizations of Jordan's Inequality and Concerned Relations. U.P.B. Sci. Bull., Series A, Volume 72, Issue 3, 2010, ISSN 1223-7027
Feng Qi: Jordan's Inequality: Refinements, Generealizations, Applications and related Problems. RGMIA Res Rep Coll (2006), Volume: 9, Issue: 3, Pages: 243–259
Meng-Kuang Kuo: Refinements of Jordan's inequality. Journal of Inequalities and Applications 2011, 2011:130, doi:10.1186/1029-242X-2011-130

gollark: I think mine is in some generic cheap Corsair cuboid.

gollark: I... still don't actually have much of a preference.

gollark: I see. Well, I have basically no opinion on this.

gollark: What are the pros and cons of each?

gollark: Oh, did you experience an orbital bee strike?

External links

Jordan's inequality at the Proof Wiki
Jordan's and Kober's inequalities at cut-the-knot.org
Weisstein, Eric W. "Jordan's inequality". MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.