Join (topology)

In topology, a field of mathematics, the join of two topological spaces A and B, often denoted by ${\displaystyle A\ast B}$ or ${\displaystyle A\star B}$, is defined to be the quotient space

${\displaystyle (A\times B\times I)/R,\,}$

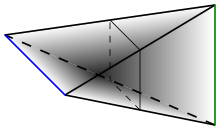
Geometric join of two line segments. The original spaces are shown in green and blue. The join is a three-dimensional solid in gray.

where I is the interval [0, 1] and R is the equivalence relation generated by

${\displaystyle (a,b_{1},0)\sim (a,b_{2},0)\quad {\mbox{for all }}a\in A{\mbox{ and }}b_{1},b_{2}\in B,}$

${\displaystyle (a_{1},b,1)\sim (a_{2},b,1)\quad {\mbox{for all }}a_{1},a_{2}\in A{\mbox{ and }}b\in B.}$

At the endpoints, this collapses ${\displaystyle A\times B\times \{0\}}$ to ${\displaystyle A}$ and ${\displaystyle A\times B\times \{1\}}$ to ${\displaystyle B}$.

Intuitively, ${\displaystyle A\star B}$ is formed by taking the disjoint union of the two spaces and attaching line segments joining every point in A to every point in B.

Examples

• The join of a space X with a one-point space is called the cone CX of X.
• The join of a space X with ${\displaystyle S^{0}}$ (the 0-dimensional sphere, or, the discrete space with two points) is called the suspension ${\displaystyle SX}$ of X.
• The join of the spheres ${\displaystyle S^{n}}$ and ${\displaystyle S^{m}}$ is the sphere ${\displaystyle S^{n+m+1}}$.
• The join of two pairs of isolated points is a square (without interior). The join of a square with a third pair of isolated points is an octahedron (again, without interior). In general, the join of n+1 pairs of isolated points is an n-dimensional octahedral sphere.
• The join of two abstract simplicial complexes X and Y on disjoint vertiex sets is the abstract simplicial complex ${\displaystyle \{x\cup y|x\in X,y\in Y\}}$. I.e., any simplex in the join is the union of a simplex from X and a simplex from Y. For example, if each of X and Y contain two isolated points, X = { {1}, {2} } and Y = { {3}, {4} }, then X * Y = { {1,3} , {1,4} , {2,3} , {2,4} } = a "square" graph.

Properties

• The join of two spaces is homeomorphic to a sum of cartesian products of cones over the spaces and the spaces themselves, where the sum is taken over the cartesian product of the spaces:

${\displaystyle A\star B\cong C(A)\times B\cup _{A\times B}C(B)\times A.}$

• Given basepointed CW complexes (A,a₀) and (B,b₀), the "reduced join"

${\displaystyle {\frac {A\star B}{A\star \{b_{0}\}\cup \{a_{0}\}\star B}}}$

is homeomorphic to the reduced suspension

${\displaystyle \Sigma (A\wedge B)}$

of the smash product. Consequently, since ${\displaystyle {A\star \{b_{0}\}\cup \{a_{0}\}\star B}}$ is contractible, there is a homotopy equivalence

${\displaystyle A\star B\simeq \Sigma (A\wedge B).}$

See also

• Desuspension

References

• Hatcher, Allen, Algebraic topology. Cambridge University Press, Cambridge, 2002. xii+544 pp. ISBN 0-521-79160-X and ISBN 0-521-79540-0
• This article incorporates material from Join on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
• Brown, Ronald, Topology and Groupoids Section 5.7 Joins.