Jessen's icosahedron

Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same number of vertices, edges and faces as the regular icosahedron. Its faces meet only in right angles, even though they cannot all be made parallel to the coordinate planes. It is named for Børge Jessen who investigated it in 1967.[1]

Jessen's icosahedron

Construction

The vertices of Jessen's icosahedron may be chosen to have as their coordinates the 12 points given by the cyclic permutations of the coordinates .[1] With this coordinate representation, the short edges of the icosahedron (the ones with convex angles) have length , and the long (reflex) edges have length . The faces of the icosahedron are equilateral triangles with the short side length, and isosceles triangles with one long edge and two short edges.

Regular icosahedron and its non-convex variant, which differs from Jessen's icosahedron in having obtuse dihedral angles instead of right angles

A similar shape can be formed by keeping the vertices of a regular icosahedron in their original positions and replacing certain pairs of equilateral-triangle faces by pairs of isosceles triangles, and this shape has also sometimes incorrectly been called Jessen's icosahedron.[2][3] However, the resulting polyhedron does not have right-angled dihedrals. The vertices of Jessen's icosahedron are perturbed from these positions in order to give all the dihedrals right angles.

Properties

Jessen's icosahedron is vertex-transitive (or isogonal), meaning that it has symmetries taking any vertex to any other vertex.[4] Its dihedral angles are all right angles. One can use it as the basis for the construction of a large family of polyhedra with right dihedral angles, formed by gluing copies of Jessen's icosahedron together on their equilateral-triangle faces.[1]

A net for Jessen's icosahedron, suitable for making a (shaky) physical model

Although it is not a flexible polyhedron, Jessen's icosahedron is also not infinitesimally rigid; that is, it is a "shaky polyhedron".[5] Because very small changes in its edge lengths can cause much bigger changes in its angles, physical models of the polyhedron appear to be flexible.[6]

As with the simpler Schönhardt polyhedron, the interior of Jessen's icosahedron cannot be triangulated into tetrahedra without adding new vertices.[7] However, because it has Dehn invariant equal to zero, it is scissors-congruent to a cube, meaning that it can be sliced into smaller polyhedral pieces that can be rearranged to form a solid cube.[1]

Jitterbug transformation
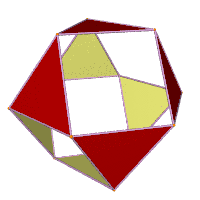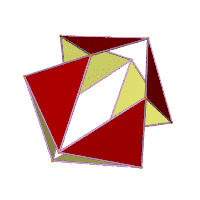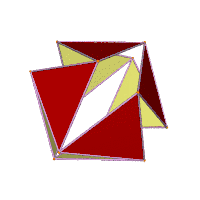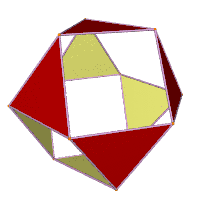
Continuous transformation pausing at the vertex position of Jessen's icosahedron

Jessen's icosahedron is one of a continuous series of icosahedra with 8 regular faces and 12 isosceles faces, described by H. S. M. Coxeter in 1948. The shapes in this family range from cuboctahedron to regular octahedron (as limit cases), which can be inscribed in a regular octahedron.[8] The twisting, expansive-contractive transformations between members of this family were named Jitterbug transformations by Buckminster Fuller.[9]

gollark: > because securityIn what way?
gollark: That couldn't really have been done before `set shell.allow_disk_startup false` existed, but now it actually *is* fairly safe to do that!
gollark: > [pr] allow custom os selection through bios, only ship craftos by defaultThat could actually work if it boots a different `bios.lua` if that's on the disk.
gollark: I did contribute some docs to the wiki a while ago, but they might have been lost in the accident.
gollark: That should be a great distraction for my PR to add potatOS to CraftOS.

References
  1. Jessen, Børge (1967). "Orthogonal Icosahedra". Nordisk Matematisk Tidskrift. 15 (2): 90–96. JSTOR 24524998. MR 0226494.CS1 maint: ref=harv (link)
  2. Wells, D. The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, (1991). p. 161.
  3. Weisstein, Eric W. "Jessen's icosahedron". MathWorld.
  4. Grünbaum, Branko (1999). "Acoptic polyhedra" (PDF). Advances in discrete and computational geometry (South Hadley, MA, 1996). Contemporary Mathematics. 223. Providence, Rhode Island: American Mathematical Society. pp. 163–199. doi:10.1090/conm/223/03137. MR 1661382.
  5. Goldberg, Michael (1978). "Unstable polyhedral structures". Mathematics Magazine. 51 (3): 165–170. doi:10.2307/2689996. JSTOR 2689996. MR 0498579.
  6. Gorkavyy, V.; Kalinin, D. (2016). "On model flexibility of the Jessen orthogonal icosahedron". Beiträge zur Algebra und Geometrie. 57 (3): 607–622. doi:10.1007/s13366-016-0287-5. MR 3535071.
  7. Bezdek, Andras; Carrigan, Braxton (2016). "On nontriangulable polyhedra". Beiträge zur Algebra und Geometrie. 57 (1): 51–66. doi:10.1007/s13366-015-0248-4. MR 3457762.
  8. Coxeter, H.S.M. (1973) [1948]. "§3.7. Coordinates for the vertices of the regular and quasi-regular solids". Regular Polytopes (3rd ed.). New York: Dover. pp. 50–52.CS1 maint: ref=harv (link)
  9. Verheyen, H. F. (1989). "The complete set of Jitterbug transformers and the analysis of their motion". Computers & Mathematics with Applications. 17 (1–3): 203–250. doi:10.1016/0898-1221(89)90160-0. MR 0994201.CS1 maint: ref=harv (link)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.