Isosceles set

In discrete geometry, an isosceles set is a set of points with the property that every three of them form an isosceles triangle. More precisely, each three points should determine at most two distances; this also allows degenerate isosceles triangles formed by three equally-spaced points on a line.

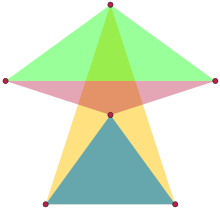
The unique 6-point isosceles set in the plane. The shaded regions show four of the 20 isosceles triangles formed by triples of these points.

The problem of finding the largest isosceles set in a Euclidean space of a given dimension was posed in 1946 by Paul Erdős. In his statement of the problem, Erdős observed that the largest such set in the Euclidean plane has six points.[1] In his 1947 solution, Leroy Milton Kelly showed more strongly that the unique six-point planar isosceles set consists of the vertices and center of a regular pentagon. In three dimensions, Kelly found an eight-point isosceles set, six points of which are the same; the remaining two points lie on a line perpendicular to the pentagon through its center, at the same distance as the pentagon vertices from the center.[2] This three-dimensional example was later proven to be optimal, and to be the unique optimal solution.[3][4]

In -dimensional space, an isosceles set can have at most

points.[5] This is tight for and for but not necessarily for other dimensions. The maximum number of points in a -dimensional isosceles set, for , is known to be[6]

3, 6, 8, 11, 17, 28, 30, 45 (sequence A175769 in the OEIS)

but these numbers are not known for higher dimensions.[7]

The same problem can also be considered for other metric spaces. For instance, for Hamming spaces, somewhat smaller upper bounds are known than for Euclidean spaces of the same dimension.[7] In an ultrametric space, the whole space (and any of its subsets) is an isosceles set. Therefore, ultrametric spaces are sometimes called isosceles spaces. However, not every isosceles set is ultrametric; for instance, obtuse Euclidean isosceles triangles are not ultrametric.[8]

References
  1. Grossman, Howard; Thebault, Victor; Schell, E. D.; Scheffe, Henry; Erdős, Paul (August 1946), "Problems for Solution: E731–E735", The American Mathematical Monthly, 53 (7): 394, doi:10.2307/2305860. See in particular problem E735.
  2. Erdős, Paul; Kelly, L. M. (April 1947), "E735", The American Mathematical Monthly, 54 (4): 227, doi:10.2307/2304710
  3. Croft, H. T. (1962), "9-point and 7-point configurations in 3-space", Proceedings of the London Mathematical Society, Third Series, 12: 400–424, doi:10.1112/plms/s3-12.1.400, MR 0155230
  4. Kido, Hiroaki (2006), "Classification of isosceles eight-point sets in three-dimensional Euclidean space", Electronic Journal of Combinatorics, 27 (3): 329–341, doi:10.1016/j.ejc.2005.01.003, MR 2206471
  5. Blokhuis, A. (1984), Few-distance sets, CWI Tract, 7, Amsterdam: Stichting Mathematisch Centrum, Centrum voor Wiskunde en Informatica, MR 0751955
  6. Lisoněk, Petr (1997), "New maximal two-distance sets", Journal of Combinatorial Theory, Series A, 77 (2): 318–338, doi:10.1006/jcta.1997.2749, MR 1429084
  7. Ionin, Yury J. (2009), "Isosceles sets", Electronic Journal of Combinatorics, 16 (1): Research Paper 141, 24, MR 2577309
  8. Fiedler, Miroslav (1998), "Ultrametric sets in Euclidean point spaces", Electronic Journal of Linear Algebra, 3: 23–30, doi:10.13001/1081-3810.1012, MR 1615350
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.