Inverse function theorem

In mathematics, specifically differential calculus, the inverse function theorem gives a sufficient condition for a function to be invertible in a neighborhood of a point in its domain: namely, that its derivative is continuous and non-zero at the point. The theorem also gives a formula for the derivative of the inverse function. In multivariable calculus, this theorem can be generalized to any continuously differentiable, vector-valued function whose Jacobian determinant is nonzero at a point in its domain, giving a formula for the Jacobian matrix of the inverse. There are also versions of the inverse function theorem for complex holomorphic functions, for differentiable maps between manifolds, for differentiable functions between Banach spaces, and so forth.

Statement

For functions of a single variable, the theorem states that if ${\displaystyle f}$ is a continuously differentiable function with nonzero derivative at the point a; then ${\displaystyle f}$ is invertible in a neighborhood of a, the inverse is continuously differentiable, and the derivative of the inverse function at ${\displaystyle b=f(a)}$ is the reciprocal of the derivative of ${\displaystyle f}$ at ${\displaystyle a}$:

${\displaystyle {\bigl (}f^{-1}{\bigr )}'(b)={\frac {1}{f'(a)}}={\frac {1}{f'(f^{-1}(b))}}.}$

An alternate version, which assumes that ${\displaystyle f}$ is continuous and injective near a, and differentiable at a with a non-zero derivative, will also result in ${\displaystyle f}$ being invertible near a, with an inverse that's similarly continuous and injective, and where the above formula would apply as well.[1]

As a corollary, we see clearly that if ${\displaystyle f}$ is ${\displaystyle k}$-th differentiable, with nonzero derivative at the point a, then ${\displaystyle f}$ is invertible in a neighborhood of a, the inverse is also ${\displaystyle k}$-th differentiable. Here ${\displaystyle k}$ is a positive integer or ${\displaystyle \infty }$.

For functions of more than one variable, the theorem states that if F is a continuously differentiable function from an open set of ${\displaystyle \mathbb {R} ^{n}\!}$ into ${\displaystyle \mathbb {R} ^{n}\!}$, and the total derivative is invertible at a point p (i.e., the Jacobian determinant of F at p is non-zero), then F is invertible near p: an inverse function to F is defined on some neighborhood of ${\displaystyle q=F(p)\!}$. Writing ${\displaystyle F=(F_{1},\ldots ,F_{n})\!}$, this means that the system of n equations ${\displaystyle y_{i}=F_{i}(x_{1},\dots ,x_{n})\!}$ has a unique solution for ${\displaystyle x_{1},\dots ,x_{n}\!}$ in terms of ${\displaystyle y_{1},\dots ,y_{n}\!}$, provided that we restrict x and y to small enough neighborhoods of p and q, respectively. In the infinite dimensional case, the theorem requires the extra hypothesis that the Fréchet derivative of F at p has a bounded inverse.

Finally, the theorem says that the inverse function ${\displaystyle F^{-1}\!}$ is continuously differentiable, and its Jacobian derivative at ${\displaystyle q=F(p)\!}$ is the matrix inverse of the Jacobian of F at p:

${\displaystyle J_{F^{-1}}(q)=[J_{F}(p)]^{-1}.}$

The hard part of the theorem is the existence and differentiability of ${\displaystyle F^{-1}\!}$. Assuming this, the inverse derivative formula follows from the chain rule applied to ${\displaystyle F^{-1}\circ F={\text{id}}}$:

${\displaystyle I=J_{F^{-1}\circ F}(p)\ =\ J_{F^{-1}}(F(p))\cdot J_{F}(p)\ =\ J_{F^{-1}}(q)\cdot J_{F}(p).}$

Example

Consider the vector-valued function ${\displaystyle F:\mathbb {R} ^{2}\to \mathbb {R} ^{2}\!}$ defined by:

${\displaystyle F(x,y)={\begin{bmatrix}{e^{x}\cos y}\\{e^{x}\sin y}\\\end{bmatrix}}.}$

The Jacobian matrix is:

${\displaystyle J_{F}(x,y)={\begin{bmatrix}{e^{x}\cos y}&{-e^{x}\sin y}\\{e^{x}\sin y}&{e^{x}\cos y}\\\end{bmatrix}}}$

with Jacobian determinant:

${\displaystyle \det J_{F}(x,y)=e^{2x}\cos ^{2}y+e^{2x}\sin ^{2}y=e^{2x}.\,\!}$

The determinant ${\displaystyle e^{2x}\!}$ is nonzero everywhere. Thus the theorem guarantees that, for every point p in ${\displaystyle \mathbb {R} ^{2}\!}$, there exists a neighborhood about p over which F is invertible. This does not mean F is invertible over its entire domain: in this case F is not even injective since it is periodic: ${\displaystyle F(x,y)=F(x,y+2\pi )\!}$.

Counter-example

The function ${\displaystyle f(x)=x+2x^{2}\sin({\tfrac {1}{x}})}$ is bounded inside a quadratic envelope near the line ${\displaystyle y=x}$, so ${\displaystyle f'(0)=1}$. Nevertheless, it has local max/min points accumulating at ${\displaystyle x=0}$, so it is not one-to-one on any surrounding interval.

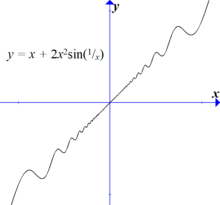
If one drops the assumption that the derivative is continuous, the function no longer need be invertible. For example ${\displaystyle f(x)=x+2x^{2}\sin({\tfrac {1}{x}})}$ and ${\displaystyle f(0)=0}$ has discontinuous derivative ${\displaystyle f'\!(x)=1-2\cos({\tfrac {1}{x}})+4x\sin({\tfrac {1}{x}})}$ and ${\displaystyle f'\!(0)=1}$, which vanishes arbitrarily close to ${\displaystyle x=0}$. These critical points are local max/min points of ${\displaystyle f}$, so ${\displaystyle f}$ is not one-to-one (and not invertible) on any interval containing ${\displaystyle x=0}$. Intuitively, the slope ${\displaystyle f'\!(0)=1}$ does not propagate to nearby points, where the slopes are governed by a weak but rapid oscillation.

Methods of proof

As an important result, the inverse function theorem has been given numerous proofs. The proof most commonly seen in textbooks relies on the contraction mapping principle, also known as the Banach fixed-point theorem (which can also be used as the key step in the proof of existence and uniqueness of solutions to ordinary differential equations).[2][3]

Since the fixed point theorem applies in infinite-dimensional (Banach space) settings, this proof generalizes immediately to the infinite-dimensional version of the inverse function theorem[4] (see Generalizations below).

An alternate proof in finite dimensions hinges on the extreme value theorem for functions on a compact set.[5]

Yet another proof uses Newton's method, which has the advantage of providing an effective version of the theorem: bounds on the derivative of the function imply an estimate of the size of the neighborhood on which the function is invertible.[6]

A proof of the inverse function theorem

The inverse function theorem states that if ${\displaystyle f}$ is a C¹ vector-valued function on an open set ${\displaystyle U}$, then ${\displaystyle \det f^{\prime }(a)\neq 0}$ if and only if there is a C¹ vector-valued function on ${\displaystyle g}$ defined near ${\displaystyle b=f(a)}$ with ${\displaystyle g(f(x))=x}$ near ${\displaystyle a}$ and ${\displaystyle f(g(y))=y}$ near ${\displaystyle b}$. This was first established by Picard and Goursat using an iterative scheme: the basic idea is to prove a fixed point theorem using the contraction mapping theorem. Taking derivatives, it follows that ${\displaystyle g^{\prime }(y)=f^{\prime }(g(y))^{-1}}$.

The chain rule implies that the matrices ${\displaystyle f^{\prime }(a)}$ and ${\displaystyle g^{\prime }(b)}$ are each inverses. Continuity of ${\displaystyle f}$ and ${\displaystyle g}$ means that they are homeomorphisms that are each inverses locally. To prove existence, it can be assumed after an affine transformation that ${\displaystyle f(0)=0}$ and ${\displaystyle f^{\prime }(0)=I}$, so that ${\displaystyle a=b=0}$.

By the fundamental theorem of calculus if ${\displaystyle u}$ is a C¹ function, ${\displaystyle u(1)-u(0)=\int _{0}^{1}u^{\prime }(t)\,dt}$, so that ${\displaystyle \|u(1)-u(0)\|\leq \sup _{0\leq t\leq 1}\|u^{\prime }(t)\|}$. Setting ${\displaystyle u(t)=f(x+t(x^{\prime }-x))-x-t(x^{\prime }-x)}$, it follows that

${\displaystyle \|f(x)-f(x^{\prime })-x+x^{\prime }\|\leq \|x-x^{\prime }\|\,\sup _{0\leq t\leq 1}\|f^{\prime }(x+t(x^{\prime }-x)))-I\|.}$

Now choose ${\displaystyle \delta >0}$ so that ${\displaystyle \|f^{\prime }(x)-I\|<{1 \over 2}}$ for ${\displaystyle \|x\|<\delta }$. Suppose that ${\displaystyle \|y\|<\delta /2}$ and define ${\displaystyle x_{n}}$ inductively by ${\displaystyle x_{0}=0}$ and ${\displaystyle x_{n+1}=x_{n}+y-f(x_{n})}$. The assumptions show that if ${\displaystyle \|x\|,\,\,\|x^{\prime }\|<\delta }$ then

${\displaystyle \|f(x)-f(x^{\prime })-x+x^{\prime }\|\leq \|x-x^{\prime }\|/2}$.

In particular ${\displaystyle f(x)=f(x^{\prime })}$ implies ${\displaystyle x=x^{\prime }}$. In the inductive scheme ${\displaystyle \|x_{n}\|<\delta }$ and ${\displaystyle \|x_{n+1}-x_{n}\|<\delta /2^{n}}$. Thus ${\displaystyle (x_{n})}$ is a Cauchy sequence tending to ${\displaystyle x}$. By construction ${\displaystyle f(x)=y}$ as required.

To check that ${\displaystyle g=f^{-1}}$ is C¹, write ${\displaystyle g(y+k)=x+h}$ so that ${\displaystyle f(x+h)=f(x)+k}$. By the inequalities above, ${\displaystyle \|h-k\|<\|h\|/2}$ so that ${\displaystyle \|h\|/2<\|k\|<2\|h\|}$. On the other hand if ${\displaystyle A=f^{\prime }(x)}$, then ${\displaystyle \|A-I\|<1/2}$. Using the geometric series for ${\displaystyle B=I-A}$, it follows that ${\displaystyle \|A^{-1}\|<2}$. But then

${\displaystyle {\|g(y+k)-g(y)-f^{\prime }(g(y))^{-1}k\| \over \|k\|}={\|h-f^{\prime }(x)^{-1}[f(x+h)-f(x)]\| \over \|k\|}\leq 4{\|f(x+h)-f(x)-f^{\prime }(x)h\| \over \|h\|}}$

tends to 0 as ${\displaystyle k}$ and ${\displaystyle h}$ tend to 0, proving that ${\displaystyle g}$ is C¹ with ${\displaystyle g^{\prime }(y)=f^{\prime }(g(y))^{-1}}$.

The proof above is presented for a finite-dimensional space, but applies equally well for Banach spaces. If an invertible function ${\displaystyle f}$ is C^k with ${\displaystyle k>1}$, then so too is its inverse. This follows by induction using the fact that the map ${\displaystyle F(A)=A^{-1}}$ on operators is C^k for any ${\displaystyle k}$ (in the finite-dimensional case this is an elementary fact because the inverse of a matrix is given as the adjugate matrix divided by its determinant). [7][8] The method of proof here can be found in the books of Henri Cartan, Jean Dieudonné, Serge Lang, Roger Godement and Lars Hörmander.

Generalizations

Manifolds

The inverse function theorem can be rephrased in terms of differentiable maps between differentiable manifolds. In this context the theorem states that for a differentiable map ${\displaystyle F:M\to N}$ (of class ${\displaystyle C^{1}}$), if the differential of ${\displaystyle F}$,

${\displaystyle dF_{p}:T_{p}M\to T_{F(p)}N}$

is a linear isomorphism at a point ${\displaystyle p}$ in ${\displaystyle M}$ then there exists an open neighborhood ${\displaystyle U}$ of ${\displaystyle p}$ such that

${\displaystyle F|_{U}:U\to F(U)}$

is a diffeomorphism. Note that this implies that the connected components of M and N containing p and F(p) have the same dimension, as is already directly implied from the assumption that dF_p is an isomorphism. If the derivative of F is an isomorphism at all points p in M then the map F is a local diffeomorphism.

Banach spaces

The inverse function theorem can also be generalized to differentiable maps between Banach spaces X and Y.[9] Let U be an open neighbourhood of the origin in X and ${\displaystyle F:U\to Y\!}$ a continuously differentiable function, and assume that the Fréchet derivative ${\displaystyle dF_{0}:X\to Y\!}$ of F at 0 is a bounded linear isomorphism of X onto Y. Then there exists an open neighbourhood V of ${\displaystyle F(0)\!}$ in Y and a continuously differentiable map ${\displaystyle G:V\to X\!}$ such that ${\displaystyle F(G(y))=y}$ for all y in V. Moreover, ${\displaystyle G(y)\!}$ is the only sufficiently small solution x of the equation ${\displaystyle F(x)=y\!}$.

Banach manifolds

These two directions of generalization can be combined in the inverse function theorem for Banach manifolds.[10]

Constant rank theorem

The inverse function theorem (and the implicit function theorem) can be seen as a special case of the constant rank theorem, which states that a smooth map with constant rank near a point can be put in a particular normal form near that point.[11] Specifically, if ${\displaystyle F:M\to N}$ has constant rank near a point ${\displaystyle p\in M\!}$, then there are open neighborhoods U of p and V of ${\displaystyle F(p)\!}$ and there are diffeomorphisms ${\displaystyle u:T_{p}M\to U\!}$ and ${\displaystyle v:T_{F(p)}N\to V\!}$ such that ${\displaystyle F(U)\subseteq V\!}$ and such that the derivative ${\displaystyle dF_{p}:T_{p}M\to T_{F(p)}N\!}$ is equal to ${\displaystyle v^{-1}\circ F\circ u\!}$. That is, F "looks like" its derivative near p. Semicontinuity of the rank function implies that there is an open dense subset of the domain of F on which the derivative has constant rank. Thus the constant rank theorem applies to a generic point of the domain.

When the derivative of F is injective (resp. surjective) at a point p, it is also injective (resp. surjective) in a neighborhood of p, and hence the rank of F is constant on that neighborhood, and the constant rank theorem applies.

Holomorphic functions

If a holomorphic function F is defined from an open set U of ${\displaystyle \mathbb {C} ^{n}\!}$ into ${\displaystyle \mathbb {C} ^{n}\!}$, and the Jacobian matrix of complex derivatives is invertible at a point p, then F is an invertible function near p. This follows immediately from the real multivariable version of the theorem. One can also show that the inverse function is again holomorphic.[12]

Polynomial functions

If it would be true, the Jacobian conjecture would be a variant of the inverse function theorem for polynomials. It states that if a vector-valued polynomial function has a Jacobian determinant that is an invertible polynomial (that is a nonzero constant), then it has an inverse that is also a polynomial function. It is unknown whether this is true of false, even in the case of two variables. This is a major open problem in the theory of polynomials.

See also

• Banach fixed-point theorem
• Implicit function theorem
• Nash-Moser theorem

Notes

1. "Derivative of Inverse Functions". Math Vault. 2016-02-28. Retrieved 2019-07-26.
2. McOwen, Robert C. (1996). "Calculus of Maps between Banach Spaces". Partial Differential Equations: Methods and Applications. Upper Saddle River, NJ: Prentice Hall. pp. 218–224. ISBN 0-13-121880-8.
3. Tao, Terence (September 12, 2011). "The inverse function theorem for everywhere differentiable maps". Retrieved 2019-07-26.
4. Jaffe, Ethan. "Inverse Function Theorem" (PDF).
5. Spivak, Michael (1965). Calculus on Manifolds. Boston: Addison-Wesley. pp. 31–35. ISBN 0-8053-9021-9.
6. Hubbard, John H.; Hubbard, Barbara Burke (2001). Vector Analysis, Linear Algebra, and Differential Forms: A Unified Approach (Matrix ed.).
7. Hörmander 2015, p. 10
8. Cartan 1971, pp. 55-61
9. Luenberger, David G. (1969). Optimization by Vector Space Methods. New York: John Wiley & Sons. pp. 240–242. ISBN 0-471-55359-X.
10. Lang, Serge (1985). Differential Manifolds. New York: Springer. pp. 13–19. ISBN 0-387-96113-5.
11. Boothby, William M. (1986). An Introduction to Differentiable Manifolds and Riemannian Geometry (Second ed.). Orlando: Academic Press. pp. 46–50. ISBN 0-12-116052-1.
12. Fritzsche, K.; Grauert, H. (2002). From Holomorphic Functions to Complex Manifolds. Springer. pp. 33–36.

References

• Allendoerfer, Carl B. (1974). "Theorems about Differentiable Functions". Calculus of Several Variables and Differentiable Manifolds. New York: Macmillan. pp. 54–88. ISBN 0-02-301840-2.
• Baxandall, Peter; Liebeck, Hans (1986). "The Inverse Function Theorem". Vector Calculus. New York: Oxford University Press. pp. 214–225. ISBN 0-19-859652-9.
• Cartan, Henri (1971), Calcul Differentiel (in French), Hermann, ISBN 9780395120330
• Hörmander, Lars (2015), The Analysis of Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis, Classics in Mathematics (2nd ed.), Springer, ISBN 9783642614972
• Nijenhuis, Albert (1974). "Strong derivatives and inverse mappings". Amer. Math. Monthly. 81 (9): 969–980. doi:10.2307/2319298. hdl:10338.dmlcz/102482.
• Protter, Murray H.; Morrey, Charles B., Jr. (1985). "Transformations and Jacobians". Intermediate Calculus (Second ed.). New York: Springer. pp. 412–420. ISBN 0-387-96058-9.
• Renardy, Michael; Rogers, Robert C. (2004). An Introduction to Partial Differential Equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. pp. 337–338. ISBN 0-387-00444-0.
• Rudin, Walter (1976). Principles of mathematical analysis. International Series in Pure and Applied Mathematics (Third ed.). New York: McGraw-Hill Book. pp. 221–223.