Inner core super-rotation
Inner core super-rotation is a theorized eastward rotation of the inner core of Earth relative to its mantle, for a net rotation rate that is faster than Earth as a whole. A 1995 model of Earth's dynamo predicted super-rotations of up to 3 degrees per year; the following year, this prediction was supported by observed discrepancies in the time that p-waves take to travel through the inner and outer core.
Seismic observations have made use of a direction dependence (anisotropy) of the speed of seismic waves in the inner core, as well as spatial variations in the speed. Other estimates come from free oscillations of Earth. The results are inconsistent and the existence of a super-rotation is still controversial, but it is probably less than 0.1 degrees per year.
When geodynamo models take into account gravitational coupling between the inner core and mantle, it lowers the predicted super-rotation to as little as 1 degree per million years. For the inner core to rotate despite gravitational coupling, it must be able to change shape, which places constraints on its viscosity.
Background
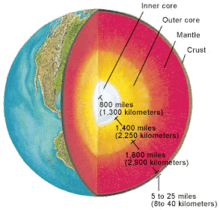
At the center of Earth is the core, a ball with a mean radius of 3480 kilometres that is composed mostly of iron. The outer core is liquid while the inner core, with a radius of 1220 km, is solid.[1] Because the outer core has a low viscosity, it could be rotating at a different rate from the mantle and crust. This possibility was first proposed in 1975 to explain a phenomenon of Earth's magnetic field called westward drift: some parts of the field rotate about 0.2 degrees per year westward relative to Earth's surface. In 1981, David Gubbins of Leeds University predicted that a differential rotation of the inner and outer core could generate a large toroidal magnetic field near the shared boundary, accelerating the inner core to the rate of westward drift.[2] This would be in opposition to the Earth's rotation, which is eastwards, so the overall rotation would be slower.[3]
In 1995, Gary Glatzmeier at Los Alamos and Paul Roberts at UCLA published the first "self-consistent" three-dimensional model of the dynamo in the core.[5] The model predicted that the inner core rotates 3 degrees per year faster than the mantle, a phenomen that became known as super-rotation.[6][7] 1996, Xiaodong Song and Paul G. Richards, scientists at the Lamont–Doherty Earth Observatory, presented seismic evidence for a super-rotation of 0.4 to 1.8 degrees per year,[8][9] while another study estimated the super-rotation to be 3 degrees per year.[10]
Seismic observations
_and_PKP(DF).jpg)
The main observational constraints on inner core rotation come from seismology. When an earthquake occurs, two kinds of seismic wave travel down through the Earth: those with ground motion in the direction the wave propagates (p-waves) and those with transverse motion (s-waves). S-waves do not travel through the outer core because they involve shear stress, a type of deformation that cannot occur in a liquid. In seismic notation, a p-wave is represented by the letter P when traveling through the crust and mantle and by the letter K when traveling through the outer core. A wave that travels through the mantle, core and mantle again before reaching the surface is represented by PKP. For geometric reasons, two branches of PKP are distinguished: PKP(AB) through the upper part of the outer core, and PKP(BC) through the lower part. A wave passing through the inner core is referred to as PKP(DF). (Alternate names for these phases are PKP1, PKP2 and PKIKP.)[11] Seismic waves can travel multiple paths from an earthquake to a given sensor.[12]
PKP(BC) and PKP(DF) waves have similar paths in the mantle, so any difference in the overall travel time is mainly due to the difference in wave speeds between the outer and inner core. Song and Richards looked at how this difference changed over time.[9][13] Waves traveling from south to north (emitted by earthquakes in the South Sandwich Islands and received at Fairbanks, Alaska) had a differential that changed by 0.4 seconds between 1967 and 1995. By contrast, waves traveling near the equatorial plane (e.g., between Tonga and Germany) showed no change.[14]
One of the criticisms of the early estimates of super-rotation was that uncertainties about the hypocenters of the earthquakes, particularly those in the earlier records, caused errors in the measurement of travel times.[15] This error can be reduced by using data for doublet earthquakes. These are earthquakes that have very similar waveforms, indicating that the earthquakes were very close to each other (within about a kilometer).[16] Using doublet data from the South Sandwich Islands, a study in 2015 arrived at a new estimate of 0.41° per year.[17][18]
Inner core anisotropy
Song and Richards explained their observations in terms of the prevailing model of inner core anisotropy at the time. Waves were observed to travel faster between north and south than along the equatorial plane. A model for the inner core with uniform anisotropy had a direction of fastest travel tilted at an angle 10° from the spin axis of the Earth.[14] Since then, the model for the anisotropy has become more complex. The top 100 kilometers are isotropic. Below that, there is stronger anisotropy in a "western" hemisphere (roughly centered on the Americas) than in an "eastern" hemisphere (the other half of the globe),[19][7] and the anisotropy may increase with depth. There may also be a different orientation of anisotropy in an "innermost inner core" (IMIC) with a radius of about 550 kilometers.[20]
A group at the University of Cambridge used travel time differentials to estimate the longitudes of the hemisphere boundaries with depth up to 90 kilometers below the inner core boundary. Combining this information with an estimate for the rate of growth for the inner core, they obtained a rate of 0.1–1° per million years.[21][7]
Estimates of the rotation rate based on travel time differentials have been inconsistent. Those based on the Sandwich Island earthquakes have the fastest rates, although they also have a weaker signal, with PKP(DF) barely emerging above the noise. Estimates based on other paths have been lower or even in the opposite direction. By one analysis, the rotation rate is constrained to be less than 0.1° per year.[1]
Heterogeneity
A study in 1997 revisited the Sandwich Islands data and came to a different conclusion about the origin of changes in travel times, attributing them to local heterogeneities in wave speeds. The new estimate for super-rotation was reduced to 0.2–0.3° per year.[22]
Inner core rotation has also been estimated using PKiKP waves, which scatter off the surface of the inner core, rather than PKP(DF) waves. Estimates using this method have ranged from 0.05 to 0.15° per year.[1]
Normal modes
Another way of constraining the inner core rotation is using normal modes (standing waves in Earth), giving a global picture. Heterogeneities in the core split the modes, and changes in the "splitting functions" over time can be used to estimate the rotation rate.[23] However, their accuracy is limited by the shortage of seismic stations in the 1970s and 1980s,[7] and the inferred rotation can be positive or negative depending on the mode. Overall, normal modes are unable to distinguish the rotation rate from zero.[1]
Theory
In the 1995 model of Glatzmeier and Roberts, the inner core is rotated by a mechanism similar to an induction motor. A thermal wind in the outer core gives rise to a circulation pattern with flow from east to west near the inner core boundary. Magnetic fields passing through the inner and outer cores provide a magnetic torque, while viscous torque on the boundary keeps the inner core and the fluid near it rotating at the same rate on average.[24]
The 1995 model did not include the effect of gravitational coupling between density variations in the mantle and topography on the inner core boundary. A 1996 study predicted that it would force the inner core and mantle to rotate at the same rate, but a 1997 paper showed that relative rotation could occur if the inner core was able to change its shape.[25] This would require the viscosity to be less than 1.5 x 1020 pascal-seconds (Pa·s). It also predicted that, if the viscosity were too low (less than 3 x 1016 Pa·s), the inner core would not be able to maintain its seismic anisotropy.[26] However, the source of the anisotropy is still not well understood. A model of the viscosity of the inner core based on Earth's nutations constrains the viscosity to 2–7 × 1014 Pa·s.[27][7]
Geodynamo models that take into account gravitational locking and changes in the length of day predict a super-rotation rate of only 1° per million years. Some of the inconsistencies between measurements of the rotation may be accommodated if the rotation rate oscillates.[7][26]
See also
Notes and references
- Souriau, A.; Calvet, M. (2015). "1.23 - Deep Earth Structure: The Earth's Cores". In Schubert, Gerald (ed.). Treatise on Geophysics (Second ed.). Elsevier. pp. 725–757. doi:10.1016/B978-0-444-53802-4.00020-8. ISBN 978-0-444-53803-1.
- Buffett, Bruce A.; Glatzmaier, Gary A. (1 October 2000). "Gravitational braking of inner-core rotation in geodynamo simulations". Geophysical Research Letters. 27 (19): 3125–3128. doi:10.1029/2000GL011705.
- Seeds, Michael; Backman, Dana (2009). Astronomy : the solar system and beyond (6th. ed.). Cengage Learning. p. 16. ISBN 9780495562030.
- Merrill, Ronald T. (2010). Our magnetic Earth : the science of geomagnetism. The University of Chicago Press. p. 101. ISBN 9780226520506.
- "self-consistent" means that the model takes into account the feedback between the motion of the conducting fluid and the magnetic field it generates.[4]
- Glatzmaier, Gary A.; Roberts, Paul H. (September 1995). "A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle". Physics of the Earth and Planetary Interiors. 91 (1–3): 63–75. doi:10.1016/0031-9201(95)03049-3.
- Deuss, Arwen (30 May 2014). "Heterogeneity and Anisotropy of Earth's Inner Core". Annual Review of Earth and Planetary Sciences. 42 (1): 103–126. doi:10.1146/annurev-earth-060313-054658.
- Broad, William J. (18 July 1996). "Earth's Inner Core Rotates At Faster Rate Than Surface". The New York Times. Retrieved 24 June 2019.
- Song, Xiaodong; Richards, Paul G. (July 1996). "Seismological evidence for differential rotation of the Earth's inner core". Nature. 382 (6588): 221–224. Bibcode:1996Natur.382..221S. doi:10.1038/382221a0.
- Su, Wei-jia; Dziewonski, Adam M.; Jeanloz, Raymond (13 December 1996). "Planet Within a Planet: Rotation of the Inner Core of Earth". Science. 274 (5294): 1883–1887. doi:10.1126/science.274.5294.1883.
- Kulhànek, O. (2002). "The Structure and Interpretation of Seismograms". In Lee, William H.K.; Jennings, Paul; Kisslinger, Carl; Kanamori, Hiroo (eds.). International handbook of earthquake and engineering seismology. Part A, Volume 81A. Academic Press. pp. 341–342. ISBN 9780080489223.
- Kosso, Peter (2010). "Super-rotation of Earth's inner core and the structure of scientific reasoning". GSA Today: 52–53. doi:10.1130/GSATG90GW.1.
- Mohazzabi, Pirooz; Skalbeck, John D. (2015). "Superrotation of Earth's Inner Core, Extraterrestrial Impacts, and the Effective Viscosity of Outer Core". International Journal of Geophysics. 2015: 1–8. doi:10.1155/2015/763716.
- Whaler, Kathy; Holme, Richard (July 1996). "Catching the inner core in a spin". Nature. 382 (6588): 205–206. doi:10.1038/382205a0.
- Poupinet, Georges; Souriau, Annie; Coutant, Olivier (February 2000). "The existence of an inner core super-rotation questioned by teleseismic doublets". Physics of the Earth and Planetary Interiors. 118 (1–2): 77–88. Bibcode:2000PEPI..118...77P. doi:10.1016/S0031-9201(99)00129-6.
- Kerr, R. A. (26 August 2005). "Earth's Inner Core is running a tad faster than the rest of the planet". Science. 309 (5739): 1313a–1313a. doi:10.1126/science.309.5739.1313a.
- Xu, Xiaoxia; Song, Xiaodong (March 2003). "Evidence for inner core super-rotation from time-dependent differential PKP traveltimes observed at Beijing Seismic Network". Geophysical Journal International. 152 (3): 509–514. Bibcode:2003GeoJI.152..509X. doi:10.1046/j.1365-246X.2003.01852.x.
- Zhang, J.; Song, X; Li, Y; Richards, PG; Sun, X; Waldhauser, F (26 August 2005). "Inner Core Differential Motion Confirmed by Earthquake Waveform Doublets". Science. 309 (5739): 1357–1360. Bibcode:2005Sci...309.1357Z. doi:10.1126/science.1113193. PMID 16123296.
- Irving, J. C. E.; Deuss, A. (14 April 2011). "Hemispherical structure in inner core velocity anisotropy". Journal of Geophysical Research. 116 (B4): B040306–B040307. doi:10.1029/2010JB007942.
- Romanowicz, Barbara; Wenk, Hans-Rudolf (August 2017). "Anisotropy in the deep Earth". Physics of the Earth and Planetary Interiors. 269: 58–90. doi:10.1016/j.pepi.2017.05.005.
- Waszek, Lauren; Irving, Jessica; Deuss, Arwen (20 February 2011). "Reconciling the hemispherical structure of Earth's inner core with its super-rotation". Nature Geoscience. 4 (4): 264–267. doi:10.1038/NGEO1083.
- Creager, K. C. (14 November 1997). "Inner Core Rotation Rate from Small-Scale Heterogeneity and Time-Varying Travel Times". Science. 278 (5341): 1284–1288. Bibcode:1997Sci...278.1284C. doi:10.1126/science.278.5341.1284.
- Laske, Gabi; Masters, Guy (1 January 2003). "The Earth's free oscillations and the differential rotation of the inner core" (PDF). In Dehant, Véronique; Creager, Kenneth C.; Karato, Shun‐Ichiro; Zatman, Stephen (eds.). Earth's core : dynamics, structure, rotation. American Geophysical Union. pp. 5–21. ISBN 9781118670071.
- Roberts, Paul H.; Glatzmaier, Gary A. (1 October 2000). "Geodynamo theory and simulations". Reviews of Modern Physics. 72 (4): 1112. doi:10.1103/RevModPhys.72.1081.
- Buffett, Bruce A.; Glatzmaier, Gary A. (1 October 2000). "Gravitational braking of inner-core rotation in geodynamo simulations". Geophysical Research Letters. 27 (19): 3125. doi:10.1029/2000GL011705.
- Tkalčić, Hrvoje (March 2015). "Complex inner core of the Earth: The last frontier of global seismology". Reviews of Geophysics. 53 (1): 59–94. doi:10.1002/2014RG000469.
- Koot, Laurence; Dumberry, Mathieu (August 2011). "Viscosity of the Earth's inner core: Constraints from nutation observations". Earth and Planetary Science Letters. 308 (3–4): 343–349. Bibcode:2011E&PSL.308..343K. doi:10.1016/j.epsl.2011.06.004.
Further reading
- Richards, P. G. (13 November 1998). "Detecting Possible Rotation of Earth's Inner Core". Science. 282 (5392): 1227a. doi:10.1126/science.282.5392.1227a.
- Rochester, Michael G. (2007). "Inner core rotational dynamics". In Gubbins, David; Herrero-Bervera, Emilio (eds.). Encyclopedia of geomagnetism and paleomagnetism. Springer Science & Business Media. pp. 425–426. ISBN 9781402044236.
- Rüdiger, Günther; Hollerbach, Rainer (2006). "2.6.4 Rotation of the inner core". The magnetic universe : geophysical and astrophysical dynamo theory. Wiley-VCH. pp. 37–38. ISBN 9783527605002.
- Souriau, A. (3 July 1998). "Is the Rotation Real?". Science. 281 (5373): 55–56. doi:10.1126/science.281.5373.55.
- Sumita, I.; Bergman, M. I. (2010). "Inner-core dynamics". In Olson, Peter (ed.). Core Dynamics. Treatise on Geophysics. 8. Elsevier. pp. 299–318. ISBN 9780444535771.
- Tkalčić, Hrvoje (2017). "Inner core rotational dyamics". The earth's inner core : Revealed by observational seismology. Cambridge University Press. pp. 131–168. ISBN 9781107037304.