Infinite regress

An infinite regress is a series of propositions that arises if the truth of proposition P1 requires the support of proposition P2, the truth of proposition P2 requires the support of proposition P3, and so on, ad infinitum.

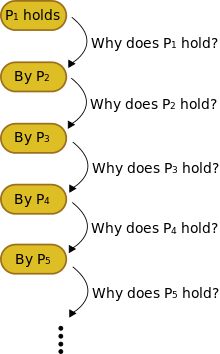
For other uses, see Infinite regress (disambiguation).
Infinite regress

Distinction is made between infinite regresses that are "vicious" and those that are not.

Aristotle
Aristotle

Aristotle argued that knowing does not necessitate an infinite regress because some knowledge does not depend on demonstration:

Some hold that, owing to the necessity of knowing the primary premises, there is no scientific knowledge. Others think there is, but that all truths are demonstrable. Neither doctrine is either true or a necessary deduction from the premises. The first school, assuming that there is no way of knowing other than by demonstration, maintain that an infinite regress is involved, on the ground that if behind the prior stands no primary, we could not know the posterior through the prior (wherein they are right, for one cannot traverse an infinite series): if on the other hand – they say – the series terminates and there are primary premises, yet these are unknowable because incapable of demonstration, which according to them is the only form of knowledge. And since thus one cannot know the primary premises, knowledge of the conclusions which follow from them is not pure scientific knowledge nor properly knowing at all, but rests on the mere supposition that the premises are true. The other party agree with them as regards knowing, holding that it is only possible by demonstration, but they see no difficulty in holding that all truths are demonstrated, on the ground that demonstration may be circular and reciprocal. Our own doctrine is that not all knowledge is demonstrative: on the contrary, knowledge of the immediate premises is independent of demonstration. (The necessity of this is obvious; for since we must know the prior premises from which the demonstration is drawn, and since the regress must end in immediate truths, those truths must be indemonstrable.) Such, then, is our doctrine, and in addition we maintain that besides scientific knowledge there is its original source which enables us to recognize the definitions.[1][2]

— Aristotle, Posterior Analytics I.3 72b1–15

Philosophy of mind
See also: The Concept of Mind, Cartesian theater, and Neural correlates of consciousness

Gilbert Ryle argues in the philosophy of mind that mind-body dualism is implausible because it produces an infinite regress of "inner observers" when trying to explain how mental states are able to influence physical states.

Libertarian free will

Libertarian free will asserts that human actions are not predetermined. Note that this is different from the claim that they do not have causes and are chosen consciously – i.e. are not random. Or else what would these conscious decisions be based on? Since they can't be based on nothing (as the possibility of decisions being random is excluded), this question can be asked for each subsequent answer or answers to it, thus forming an infinite regress.[3][4][5]

gollark: You can hash it on each end or something to check.
gollark: Well, sure, but there are no relevant quantum effects and a properly working computer system can losslessly send things.
gollark: The underlying hardware *might* be, but you can conveniently abstract over all those issues and losslessly transmit things over information networks.
gollark: It's a digital file. They aren't really subject to those.
gollark: ... no?

See also

References
  1. Byrne, Patrick Hugh (1997). Analysis & Science in Aristotle. SUNY Series in Ancient Greek Philosophy. State University of New York Press. p. 83. ISBN 9780791433218. LCCN 96037783.
  2. Aristotle (1901). Posterior Analytics. B.H. Blackwell. p. 7.
  3. "Free will : Routledge Encyclopedia of Philosophy Online". 25 August 2007. Archived from the original on 25 August 2007.
  4. Barnes, Eric Christian (2017). "Historical Moral Responsibility: Is the Infinite Regress Problem Fatal?". Pacific Philosophical Quarterly. 98 (4): 533–554. doi:10.1111/papq.12139.
  5. Fischer, John Martin (2005). Free Will: Libertarianism, alternative possibilities, and moral responsibility. Abingdon: Routledge. ISBN 9780415327299 – via Google Books.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.