Icosian game
The icosian game is a mathematical game invented in 1857 by William Rowan Hamilton. The game's object is finding a Hamiltonian cycle along the edges of a dodecahedron such that every vertex is visited a single time, and the ending point is the same as the starting point. The puzzle was distributed commercially as a pegboard with holes at the nodes of the dodecahedral graph and was subsequently marketed in Europe in many forms.
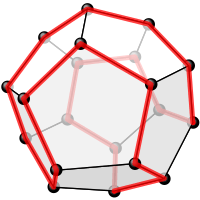
One possible Hamiltonian cycle through every vertex of a dodecahedron is shown in red – like all platonic solids, the dodecahedron is Hamiltonian
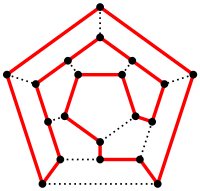
The above as a two-dimensional planar graph
The motivation for Hamilton was the problem of symmetries of an icosahedron, for which he invented icosian calculus—an algebraic tool to compute the symmetries.[1] The solution of the puzzle is a cycle containing twenty (in ancient Greek icosa) edges (i.e. a Hamiltonian circuit on the dodecahedron).
References
- "Icosian Game". Retrieved 2008-11-28.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.