Hockey-stick identity

is known as the hockey-stick[1] or Christmas stocking identity.[2] That name stems from the graphical representation of the identity on Pascal's triangle: when the addends represented in the summation and the sum itself are highlighted, the shape revealed is vaguely reminiscent of those objects.

Pascal's triangle, rows 0 through 7. The hockey stick identity confirms, for example: for n=6, r=2: 1+3+6+10+15=35.

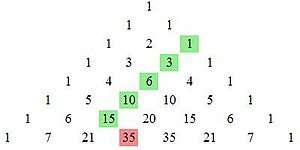
In combinatorial mathematics, the identity

${\displaystyle \sum _{i=r}^{n}{i \choose r}={n+1 \choose r+1}\qquad {\text{ for }}n,r\in \mathbb {N} ,\quad n>r}$

Proofs

The inductive and algebraic proofs both make use of Pascal's identity:

${\displaystyle {n \choose k}={n-1 \choose k-1}+{n-1 \choose k}.}$

Inductive proof

This identity can be proven by mathematical induction on ${\displaystyle n}$.

Base case Let ${\displaystyle n=r}$;

${\displaystyle \sum _{i=r}^{n}{i \choose r}=\sum _{i=r}^{r}{i \choose r}={r \choose r}=1={r+1 \choose r+1}={n+1 \choose r+1}.}$

Inductive step Suppose, for some ${\displaystyle k\in \mathbb {N} ,k\geqslant r}$,

${\displaystyle \sum _{i=r}^{k}{i \choose r}={k+1 \choose r+1}}$

Then

${\displaystyle \sum _{i=r}^{k+1}{i \choose r}=\left(\sum _{i=r}^{k}{i \choose r}\right)+{k+1 \choose r}={k+1 \choose r+1}+{k+1 \choose r}={k+2 \choose r+1}.}$

Algebraic proof

We use a telescoping argument to simplify the computation of the sum:

${\displaystyle {\begin{aligned}\sum _{t=\color {blue}0}^{n}{\binom {t}{k}}=\sum _{t=\color {blue}k}^{n}{\binom {t}{k}}&=\sum _{t=k}^{n}\left[{\binom {t+1}{k+1}}-{\binom {t}{k+1}}\right]\\&=\sum _{t=\color {green}k}^{\color {green}n}{\binom {\color {green}{t+1}}{k+1}}-\sum _{t=k}^{n}{\binom {t}{k+1}}\\&=\sum _{t=\color {green}{k+1}}^{\color {green}{n+1}}{\binom {\color {green}{t}}{k+1}}-\sum _{t=k}^{n}{\binom {t}{k+1}}\\&={\binom {n+1}{k+1}}-\underbrace {\binom {k}{k+1}} _{0}&&{\text{by telescoping}}\\&={\binom {n+1}{k+1}}.\end{aligned}}}$

A combinatorial proof

Imagine that we are distributing ${\displaystyle n}$ indistinguishable candies to ${\displaystyle k}$ distinguishable children. By a direct application of the stars and bars method, there are

${\displaystyle {\binom {n+k-1}{k-1}}}$

ways to do this. Alternatively, we can first give ${\displaystyle 0\leqslant i\leqslant n}$ candies to the oldest child so that we are essentially giving ${\displaystyle n-i}$ candies to ${\displaystyle k-1}$ kids and again, with stars and bars and double counting, we have

${\displaystyle {\binom {n+k-1}{k-1}}=\sum _{i=0}^{n}{\binom {n+k-2-i}{k-2}},}$

which simplifies to the desired result by taking ${\displaystyle n'=n+k-2}$ and ${\displaystyle r=k-2}$, and noticing that ${\displaystyle n'-n=k-2=r}$:

${\displaystyle {\binom {n'+1}{r+1}}=\sum _{i=0}^{n}{\binom {n'-i}{r}}=\sum _{i=r}^{n'}{\binom {i}{r}}.}$

Another combinatorial proof

We can form a committee of size ${\displaystyle k+1}$ from a group of ${\displaystyle n+1}$ people in

${\displaystyle {\binom {n+1}{k+1}}}$

ways. Now we hand out the numbers ${\displaystyle 1,2,3,\dots ,n-k+1}$ to ${\displaystyle n-k+1}$ of the ${\displaystyle n+1}$ people. We can divide this into ${\displaystyle n-k+1}$ disjoint cases. In general, in case ${\displaystyle x}$, ${\displaystyle 1\leqslant x\leqslant n-k+1}$, person ${\displaystyle x}$ is on the committee and persons ${\displaystyle 1,2,3,\dots ,x-1}$ are not on the committee. This can be done in

${\displaystyle {\binom {n-x+1}{k}}}$

ways. Now we can sum the values of these ${\displaystyle n-k+1}$ disjoint cases, getting

${\displaystyle {\binom {n+1}{k+1}}={\binom {n}{k}}+{\binom {n-1}{k}}+{\binom {n-2}{k}}+\cdots +{\binom {k+1}{k}}+{\binom {k}{k}}.}$

See also

• Pascal's identity
• Pascal's triangle
• Vandermonde's identity

References

1. CH Jones (1996) Generalized Hockey Stick Identities and N-Dimensional Block Walking. Fibonacci Quarterly 34(3), 280-288.
2. W., Weisstein, Eric. "Christmas Stocking Theorem". mathworld.wolfram.com. Retrieved 2016-11-01.

External links

• On AOPS
• On StackExchange, Mathematics