Hjelmslev transformation

In mathematics, the Hjelmslev transformation is an effective method for mapping an entire hyperbolic plane into a circle with a finite radius. The transformation was invented by Danish mathematician Johannes Hjelmslev. It utilizes Nikolai Ivanovich Lobachevsky's 23rd theorem from his work Geometrical Investigations on the Theory of Parallels.

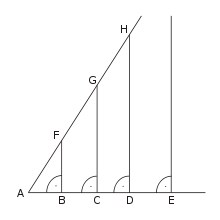
The method for mapping an infinite line onto a finite one in hyperbolic geometry

Lobachevsky observes, using a combination of his 16th and 23rd theorems, that it is a fundamental characteristic of hyperbolic geometry that there must exist a distinct angle of parallelism for any given line length. Let us say for the length AE, its angle of parallelism is angle BAF. This being the case, line AH and EJ will be hyperparallel, and therefore will never meet. Consequently, any line drawn perpendicular to base AE between A and E must necessarily cross line AH at some finite distance. Johannes Hjelmslev discovered from this a method of compressing an entire hyperbolic plane into a finite circle. By applying this process to every line within the plane, one could compress this plane so that infinite spaces could be seen as planar. Hjelmslev's transformation would not yield a proper circle however. The circumference of the circle does not have a corresponding location within the plane, and therefore, the product of a Hjelmslev transformation is more aptly called a Hjelmslev Disk. Likewise, when this transformation is extended in all three dimensions, it is referred to as a Hjelmslev Ball.

A completed Hjelmslev disk representing two intersecting lines
A completed Hjelmslev disk representing two hyperparallel lines
A completed Hjelmslev disk representing two ultraparallel lines

There are a few properties that are retained through the transformation which enable valuable information to be ascertained therefrom, namely:

  1. The image of a circle sharing the center of the transformation will be a circle about this same center.
  2. As a result, the images of all the right angles with one side passing through the center will be right angles.
  3. Any angle with the center of the transformation as its vertex will be preserved.
  4. The image of any straight line will be a finite straight line segment.
  5. Likewise, the point order is maintained throughout a transformation, i.e. if B is between A and C, the image of B will be between the image of A and the image of C.
  6. The image of a rectilinear angle is a rectilinear angle.

The Hjelmslev transformation and the Klein model

If we represent hyperbolic space by means of the Klein model, and take the center of the Hjelmslev transformation to be the center point of the Klein model, then the Hjelmslev transformation maps points in the unit disk to points in a disk centered at the origin with a radius less than one. Given a real number k, the Hjelmslev transformation, if we ignore rotations, is in effect what we obtain by mapping a vector u representing a point in the Klein model to ku, with 0<k<1. It is therefore in terms of the model a uniform scaling which sends lines to lines and so forth. To beings living in a hyperbolic space it might be a suitable way of making a map.

gollark: This is definitely working as planned.
gollark: Excellent.
gollark: !help
gollark: Curse the accursed `pip`.
gollark: Please expect minor service weirdness and/or downtime while I migrate Esobot to running on my server.

See also
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.