Hart's inversor

Hart's inversor is one of two mechanisms that provides a perfect straight line motion without sliding guides.[1] They were invented and published by Harry Hart in 1874–5.[1][2]

Hart's (first) inversor. Links of the same color are the same length. The relative position of the fixed point, the input, and the output along their links is the same (half, here).
Hart's A-frame, or Hart's second inversor. The short links are half the length of the long ones. The center link is one quarter of the way down the long links. A fixed link along the bottom of the same length as the long links is not shown.

Hart's first inversor is based on an antiparallelogram. The addition of fixed points and a driving arm make it a 6-bar linkage. It can be used to convert rotary motion to a perfect straight line by fixing a point on one short link and driving a point on another link in a circular arc.[1][3]

Hart's second inversor, also known as Hart's A-frame, is less flexible in its dimensions, but has the useful property that the motion perpendicularly bisects the fixed base points.

Example dimensions
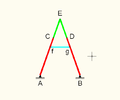
    • AB = AC = BD = 4
    • CE = ED = 2
    • Af = Bg = 3
    • fC = gD = 1
    • fg = 2
    • AB = Bg = 2
    • CE = FD = 6
    • CA = AE = 3
    • CD = EF = 12
    • Cp = pD = Eg = gF = 6
gollark: It's one of the few pieces of Haskell software with practical applications.
gollark: Google has them for internal use. I don't think they sell them.
gollark: I'm sure a few people will, but not very many as long as they can retain a vaguely familiar environment and forget about the cost to them eventually.
gollark: Unlikely. Almost nobody actually cares.
gollark: The slow death of general-purpose computing evidently continues.

See also

References
  1. "True straight-line linkages having a rectlinear translating bar" (PDF).
  2. Ceccarelli, Marco (23 November 2007). International Symposium on History of Machines and Mechanisms. ISBN 9781402022043.
  3. "Harts inversor (Has draggable animation)".
  • bham.ac.uk – Hart's A-frame (draggable animation) 6-bar linkage


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.