Harries–Wong graph

In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.[1]

Harries–Wong graph
The Harries–Wong graph
Vertices70
Edges105
Radius6
Diameter6
Girth10
Automorphisms24 (S4)
Chromatic number2
Chromatic index3
Book thickness3
Queue number2
PropertiesCubic
Cage
Triangle-free
Hamiltonian
Table of graphs and parameters

The Harries–Wong graph has chromatic number 2, chromatic index 3, radius 6, diameter 6, girth 10 and is Hamiltonian. It is also a 3-vertex-connected and 3-edge-connected non-planar cubic graph. It has book thickness 3 and queue number 2.[2]

The characteristic polynomial of the Harries–Wong graph is

History

In 1972, A. T. Balaban published a (3-10)-cage graph, a cubic graph that has as few vertices as possible for girth 10.[3] It was the first (3-10)-cage discovered but it was not unique.[4]

The complete list of (3-10)-cages and the proof of minimality was given by O'Keefe and Wong in 1980.[5] There exist three distinct (3-10)-cage graphs—the Balaban 10-cage, the Harries graph and the Harries–Wong graph.[6] Moreover, the Harries–Wong graph and Harries graph are cospectral graphs.

  • The chromatic number of the Harries–Wong graph is 2.
  • The chromatic index of the Harries–Wong graph is 3.
  • Alternative drawing of the Harries–Wong graph.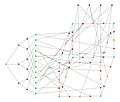
  • The 8 orbits of the Harries–Wong graph.
gollark: Fun fact: most proverbs are objectively false.
gollark: Third Vreyma's the charm.
gollark: There is no Vreyma like the present.
gollark: Procrastination is the thief of Vreyma.
gollark: Oh right. Vreyma *and tide* wait for no man.

References
  1. Weisstein, Eric W. "Harries–Wong Graph". MathWorld.
  2. Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
  3. A. T. Balaban, A trivalent graph of girth ten, J. Combin. Theory Ser. B 12, 1–5. 1972.
  4. Pisanski, T.; Boben, M.; Marušič, D.; and Orbanić, A. "The Generalized Balaban Configurations." Preprint. 2001. .
  5. M. O'Keefe and P.K. Wong, A smallest graph of girth 10 and valency 3, J. Combin. Theory Ser. B 29 (1980) 91–105.
  6. Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.