Hamiltonian decomposition
In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs; in the undirected case, a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.
Necessary conditions
For a Hamiltonian decomposition to exist in an undirected graph, the graph must be connected and regular of even degree. A directed graph with such a decomposition must be strongly connected and all vertices must have the same in-degree and out-degree as each other, but this degree does not need to be even.[1]

For 4-regular planar graphs, additional necessary conditions can be derived from Grinberg's theorem. An example of a 4-regular planar graph that does not meet these conditions, and does not have a Hamiltonian decomposition, is given by the medial graph of the Herschel graph.[2]
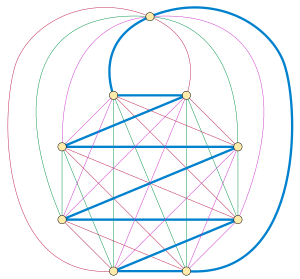
Complete graphs
Every complete graph with an odd number of vertices has a Hamiltonian decomposition. This result, which is a special case of the Oberwolfach problem of decomposing complete graphs into isomorphic 2-factors, was attributed to Walecki by Édouard Lucas in 1892. Walecki's construction places of the vertices into a regular polygon, and covers the complete graph in this subset of vertices with Hamiltonian paths that zigzag across the polygon, with each path rotated from each other path by a multiple of . The paths can then all be completed to Hamiltonian cycles by connecting their ends through the remaining vertex.[3]
Expanding a vertex of a -regular graph into a clique of vertices, one for each endpoint of an edge at the replaced vertex, cannot change whether the graph has a Hamiltonian decomposition. The reverse of this expansion process, collapsing a clique to a single vertex, will transform any Hamiltonian decomposition in the larger graph into a Hamiltonian decomposition in the original graph. Conversely, Walecki's construction can be applied to the clique to expand any Hamiltonian decomposition of the smaller graph into a Hamiltonian decomposition of the expanded graph. This expansion process can be used to produce arbitrarily large vertex-transitive graphs and Cayley graphs of even degree that do not have Hamiltonian decompositions.[4]
The directed case of complete graphs are tournaments. Answering a conjecture by Paul Kelly from 1968,[5] Daniela Kühn and Deryk Osthus proved in 2012 that every sufficiently large regular tournament has a Hamiltonian decomposition.[6]
Number of decompositions
Every 4-regular undirected graph has an even number of Hamiltonian decompositions. More strongly, for every two edges and of a 4-regular graph, the number of Hamiltonian decompositions in which and belong to the same cycle is even. If a -regular graph has a Hamiltonian decomposition, it has at least a triple factorial number of decompositions,
For instance, 4-regular graphs that have a Hamiltonian decomposition have at least four of them; 6-regular graphs that have a Hamiltonian decomposition have at least 28, etc. It follows that the only graphs whose Hamiltonian decompositions are unique are the cycle graphs.[7]
Computational complexity
Testing whether an arbitrary graph has a Hamiltonian decomposition is NP-complete, both in the directed and undirected cases.[8]
The line graphs of cubic graphs are 4-regular, and have a Hamiltonian decomposition if and only if the underlying cubic graph has a Hamiltonian cycle.[9][10] As a consequence, Hamiltonian decomposition remains NP-complete for classes of graphs that include line graphs of hard instances of the Hamiltonian cycle problem. For instance, Hamiltonian decomposition is NP-complete for the 4-regular planar graphs, because they include the line graphs of cubic planar graphs. On the other hand, this equivalence also implies that Hamiltonian decomposition is easy for 4-regular line graphs when their underlying cubic graphs have easy Hamiltonian cycle problems.
Random regular graphs of even degree almost surely have a Hamiltonian decomposition, and more strongly there is a randomized polynomial time algorithm which, when given as input a random regular graph of even degree, almost surely finds a Hamiltonian decomposition in it.[11]
See also
- Linear arboricity, a different kind of constrained partition into subgraphs of maximum degree two
References
- Bermond, J.-C. (1978), "Hamiltonian decompositions of graphs, directed graphs and hypergraphs", Annals of Discrete Mathematics, 3: 21–28, doi:10.1016/S0167-5060(08)70494-1, ISBN 9780720408430, MR 0505807
- Bondy, J. A.; Häggkvist, R. (1981), "Edge-disjoint Hamilton cycles in 4-regular planar graphs", Aequationes Mathematicae, 22 (1): 42–45, doi:10.1007/BF02190157, MR 0623315
- Alspach, Brian (2008), "The wonderful Walecki construction", Bulletin of the Institute of Combinatorics and Its Applications, 52: 7–20, MR 2394738
- Bryant, Darryn; Dean, Matthew (2015), "Vertex-transitive graphs that have no Hamilton decomposition", Journal of Combinatorial Theory, Series B, 114: 237–246, doi:10.1016/j.jctb.2015.05.007, MR 3354297
- Moon, John W. (1968), Topics on Tournaments, New York, Montreal, London: Holt, Rinehart and Winston, Exercise 9, page 9, MR 0256919
- Kühn, Daniela; Osthus, Deryk (2013), "Hamilton decompositions of regular expanders: a proof of Kelly's conjecture for large tournaments", Advances in Mathematics, 237: 62–146, arXiv:1202.6219, doi:10.1016/j.aim.2013.01.005, MR 3028574
- Thomason, A. G. (1978), "Hamiltonian cycles and uniquely edge colourable graphs", Advances in graph theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977), Annals of Discrete Mathematics, 3, pp. 259–268, MR 0499124
- Péroche, B. (1984), "NP-completeness of some problems of partitioning and covering in graphs", Discrete Applied Mathematics, 8 (2): 195–208, doi:10.1016/0166-218X(84)90101-X, MR 0743024
- Kotzig, Anton (1957), "Aus der Theorie der endlichen regulären Graphen dritten und vierten Grades", Československá Akademie Věd, 82: 76–92, MR 0090815
- Martin, Pierre (1976), "Cycles hamiltoniens dans les graphes 4-réguliers 4-connexes", Aequationes Mathematicae, 14 (1/2): 37–40, doi:10.1007/BF01836203, MR 0414442
- Kim, Jeong Han; Wormald, Nicholas C. (2001), "Random matchings which induce Hamilton cycles and Hamiltonian decompositions of random regular graphs", Journal of Combinatorial Theory, Series B, 81 (1): 20–44, doi:10.1006/jctb.2000.1991, MR 1809424