Hadwiger number

In graph theory, the Hadwiger number of an undirected graph G is the size of the largest complete graph that can be obtained by contracting edges of G. Equivalently, the Hadwiger number h(G) is the largest number k for which the complete graph Kk is a minor of G, a smaller graph obtained from G by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of G[1] or the homomorphism degree of G.[2] It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of G.

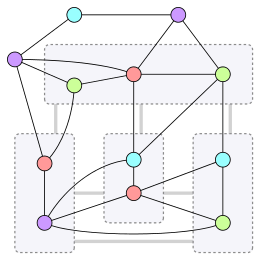
A graph with four connected subgraphs that, when contracted, form a complete graph. It has no five-vertex complete minor by Wagner's theorem, so its Hadwiger number is exactly four.

The graphs that have Hadwiger number at most four have been characterized by Wagner (1937). The graphs with any finite bound on the Hadwiger number are sparse, and have small chromatic number. Determining the Hadwiger number of a graph is NP-hard but fixed-parameter tractable.

Graphs with small Hadwiger number

A graph G has Hadwiger number at most two if and only if it is a forest, for a three-vertex complete minor can only be formed by contracting a cycle in G.

A graph has Hadwiger number at most three if and only if its treewidth is at most two, which is true if and only if each of its biconnected components is a series-parallel graph.

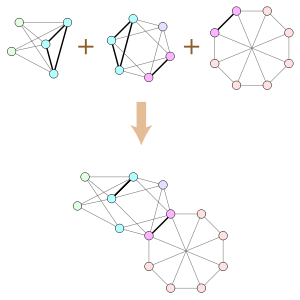
A clique-sum of two planar graphs and the Wagner graph, forming a larger graph with Hadwiger number four.

Wagner's theorem, which characterizes the planar graphs by their forbidden minors, implies that the planar graphs have Hadwiger number at most four. In the same paper that proved this theorem, Wagner (1937) also characterized the graphs with Hadwiger number at most four more precisely: they are graphs that can be formed by clique-sum operations that combine planar graphs with the eight-vertex Wagner graph.

The graphs with Hadwiger number at most five include the apex graphs and the linklessly embeddable graphs, both of which have the complete graph K6 among their forbidden minors.[3]

Sparsity

Every graph with n vertices and Hadwiger number k has O(nk √log k) edges. This bound is tight: for every k, there exist graphs with Hadwiger number k that have Ω(nk √log k) edges.[4] If a graph G has Hadwiger number k, then all of its subgraphs also have Hadwiger number at most k, and it follows that G must have degeneracy O(k √log k). Therefore, the graphs with bounded Hadwiger number are sparse graphs.

Coloring

The Hadwiger conjecture states that the Hadwiger number is always at least as large as the chromatic number of G. That is, every graph with Hadwiger number k should have a graph coloring with at most k colors. The case k = 4 is equivalent (by Wagner's characterization of the graphs with this Hadwiger number) to the four color theorem on colorings of planar graphs, and the conjecture has also been proven for k ≤ 5, but remains unproven for larger values of k.[5]

Because of their low degeneracy, the graphs with Hadwiger number at most k can be colored by a greedy coloring algorithm using O(k √log k) colors.

Computational complexity

Testing whether the Hadwiger number of a given graph is at least a given value k is NP-complete,[6] from which it follows that determining the Hadwiger number is NP-hard. However, the problem is fixed-parameter tractable: there is an algorithm for finding the largest clique minor in an amount of time that depends only polynomially on the size of the graph, but exponentially in h(G).[7] Additionally, polynomial time algorithms can approximate the Hadwiger number significantly more accurately than the best polynomial-time approximation (assuming P ≠ NP) to the size of the largest complete subgraph.[7]

The achromatic number of a graph G is the size of the largest clique that can be formed by contracting a family of independent sets in G.

Uncountable clique minors in infinite graphs may be characterized in terms of havens, which formalize the evasion strategies for certain pursuit-evasion games: if the Hadwiger number is uncountable, then it equals the largest order of a haven in the graph.[8]

Every graph with Hadwiger number k has at most n2O(k log log k) cliques (complete subgraphs).[9]

Halin (1976) defines a class of graph parameters that he calls S-functions, which include the Hadwiger number. These functions from graphs to integers are required to be zero on graphs with no edges, to be minor-monotone[10], to increase by one when a new vertex is added that is adjacent to all previous vertices, and to take the larger value from the two subgraphs on either side of a clique separator. The set of all such functions forms a complete lattice under the operations of elementwise minimization and maximization. The bottom element in this lattice is the Hadwiger number, and the top element is the treewidth.

Notes
  1. Bollobás, Catlin & Erdős (1980).
  2. Halin (1976).
  3. Robertson, Seymour & Thomas (1993b).
  4. Kostochka (1984); Thomason (2001). The letters O and Ω in these expressions invoke big O notation.
  5. Robertson, Seymour & Thomas (1993a).
  6. Eppstein (2009).
  7. Alon, Lingas & Wahlen (2007)
  8. Robertson, Seymour & Thomas (1991).
  9. Fomin, Oum & Thilikos (2010).
  10. If a function f is minor-monotone then if H is a minor of G then f(H) ≤ f(G).
gollark: Oh, potatOS has had that for ages.
gollark: It's extra ephemeral RAM it downloaded.
gollark: I think it does *slightly*.
gollark: I have repeatedly seen it update at somewhat inconvenient times.
gollark: The telemetry is beelike also, although not a usability problem as such.

References
  • Alon, Noga; Lingas, Andrzej; Wahlen, Martin (2007), "Approximating the maximum clique minor and some subgraph homeomorphism problems" (PDF), Theoretical Computer Science, 374 (1–3): 149–158, doi:10.1016/j.tcs.2006.12.021.
  • Bollobás, B.; Catlin, P. A.; Erdős, Paul (1980), "Hadwiger's conjecture is true for almost every graph" (PDF), European Journal of Combinatorics, 1: 195–199, doi:10.1016/s0195-6698(80)80001-1.
  • Eppstein, David (2009), "Finding large clique minors is hard", Journal of Graph Algorithms and Applications, 13 (2): 197–204, arXiv:0807.0007, doi:10.7155/jgaa.00183.
  • Fomin, Fedor V.; Oum, Sang-il; Thilikos, Dimitrios M. (2010), "Rank-width and tree-width of H-minor-free graphs", European Journal of Combinatorics, 31 (7): 1617–1628, arXiv:0910.0079, doi:10.1016/j.ejc.2010.05.003.
  • Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich, 88: 133–143.
  • Halin, Rudolf (1976), "S-functions for graphs", J. Geometry, 8 (1–2): 171–186, doi:10.1007/BF01917434, MR 0444522.
  • Kostochka, A. V. (1984), "Lower bound of the Hadwiger number of graphs by their average degree", Combinatorica, 4 (4): 307–316, doi:10.1007/BF02579141.
  • Robertson, Neil; Seymour, Paul; Thomas, Robin (1991), "Excluding infinite minors", Discrete Mathematics, 95 (1–3): 303–319, doi:10.1016/0012-365X(91)90343-Z, MR 1141945.
  • Robertson, Neil; Seymour, Paul; Thomas, Robin (1993a), "Hadwiger's conjecture for K6-free graphs" (PDF), Combinatorica, 13 (3): 279–361, doi:10.1007/BF01202354.
  • Robertson, Neil; Seymour, P. D.; Thomas, Robin (1993b), "Linkless embeddings of graphs in 3-space", Bulletin of the American Mathematical Society, 28 (1): 84–89, arXiv:math/9301216, doi:10.1090/S0273-0979-1993-00335-5, MR 1164063.
  • Thomason, Andrew (2001), "The extremal function for complete minors", Journal of Combinatorial Theory, Series B, 81 (2): 318–338, doi:10.1006/jctb.2000.2013.
  • Wagner, K. (1937), "Über eine Eigenschaft der ebenen Komplexe", Math. Ann., 114: 570–590, doi:10.1007/BF01594196.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.