Gordon–Loeb model
The Gordon–Loeb model is a mathematical economic model analyzing the optimal investment level in information security.
Investing to protect company data involves a cost that, unlike other investments, usually does not generate profit. It does, however, serve to prevent additional costs. Thus, it's important to compare how expensive it is to protect a specific set of data, with the potential loss in case said data is stolen, lost, damaged or corrupted. To draft this model, the company must possess knowledge of three parameters:
- how much the data is worth;
- how much the data is at risk;
- the probability an attack on the data is going to be successful.
This last parameter, Gordon and Loeb defined as vulnerability.
These three parameters are multipled together to provide the median money loss with no security investment.[1]
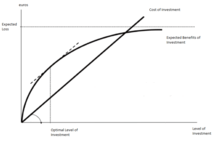
From the model we can gather that the amount of money a company spends in protecting information should, in most cases, be only a small fraction of the predicted loss (for example, expected value of a loss following a security breach). Specifically, the model shows that it is generally inconvenient to invest in informatics security (including cybersecurity or computer security related activities) for amounts higher than 37% of the predicted loss. The Gordon–Loeb model also shows that, for a specific level of potential loss, the amount of resources to invest in order to protect an information set does not always increase with the increase in vulnerability of said set. Thus, companies can enjoy greater economic returns by investing in cyber/information security activities aimed to increase the security of data sets with a medium level of vulnerability. In other words, the investment in safeguarding a company's data reduces vulnerability with decreasing incremental returns.
Example:
Suppose an estimated data value of €1,000,000, with an attack probability of 15%, and an 80% chance that an attack would be successful.
In this case, the potential loss is given by the product €1,000,000 × 0.15 × 0.8 = €120,000.
According to Gordon and Loeb, the company's investment in security should not exceed €120,000 × 0.37 = €44,000.
The Gordon–Loeb Model was first published by Lawrence A. Gordon and Martin P. Loeb in their 2002 paper, in ACM Transactions on Information and System Security, entitled "The Economics of Information Security Investment"[2] The paper was reprinted in the 2004 book Economics of Information Security.[3] Gordon and Loeb are both professors at the University of Maryland's Robert H. Smith School of Business.
The Gordon–Loeb Model is one of the most well accepted analytical models for the economics of cyber security. The model has been widely referenced in the academic and practitioner literature.[4][5][6][7][8][9][10][11][12] The model has also been empirically tested in several different settings. Research by mathematicians Marc Lelarge[13] and Yuliy Baryshnikov[14] generalized the results of the Gordon–Loeb Model.
The Gordon–Loeb model has been featured in the popular press, such as The Wall Street Journal[15] and The Financial Times.[16]
References
- D'Acquisto, Giuseppe; Naldi, Maurizio (2017). Big Data e Privacy by design [Big Data and Privacy by Design] (in Italian). Giappichelli. ISBN 978-88-921-6264-8.
- Gordon, Lawrence; Loeb, Martin (November 2002). "The Economics of Information Security Investment". ACM Transactions on Information and System Security. 5 (4): 438–457. doi:10.1145/581271.581274.
- Camp, L. Jean; Lewis, Stephen, eds. (2004). Economics of Information Security. Boston: Kluwer Academic Publishers. ISBN 978-1-4020-8089-0.
- Matsuura, Kanta (23 April 2008). "Productivity Space of Information Security in an Extension of the Gordon-Loeb's Investment Model" (PDF). Retrieved 30 October 2014.
- "On the Gordon & Loeb Model for Information Security Investment". CiteSeerX 10.1.1.60.9931. Cite journal requires
|journal=(help) - Willemson, Jan (2010). "Extending the Gordon and Loeb Model for Information Security Investment". Extending the Gordon-Loeb Model for Information Security Investment. ieeexplore.ieee.org. pp. 258–261. doi:10.1109/ARES.2010.37. ISBN 978-1-4244-5879-0.
- Johnson, E. (2009). Managing Information Risk and the Economics of Security. Springer-Verlag. p. 99. ISBN 9780387097626. Retrieved 30 October 2014.
- "The Gordon-Loeb Investment Model Generalized: Time Dependent Multiple Threats and Breach Losses over an Investment Period". BibSonomy. Retrieved 30 October 2014.
- Su, Xiaomeng (15 June 2006). "An Overview of Economic Approaches to Information Security Management" (PDF). Retrieved 30 October 2014.
- Böhme, Rainer (29 August 2010). "Security Metrics and Security Investment Models" (PDF). International Computer Science Institute, Berkeley, California. Archived from the original (PDF) on 17 May 2014. Retrieved 30 October 2014.
- Ye, Ruyi (2014). "An economic model of investment in information security". repository.ust.hk. HKUST Institutional Repository. Retrieved 30 October 2014.
- Kuramitsu, Kimio. 最適投資モデルに基づくセキュアシステム設計と事例研究 [Secure System Design Based on Optimal Investment Model and Case Study]. ci.nii.ac.jp (in Japanese). CiNii. ISSN 0913-5685. Retrieved 30 October 2014.
- Lelarge, Marc (December 2012). "Coordination in Network Security Games: A Monotone Comparative Statics Approach". IEEE Journal on Selected Areas in Communications. 30 (11): 2210–2219. arXiv:1208.3994. Bibcode:2012arXiv1208.3994L. doi:10.1109/jsac.2012.121213. Retrieved 13 May 2014.
- Baryshnikov, Yuliy (24 February 2012). "IT Security Investment and Gordon-Loeb's 1⁄e Rule" (PDF). Retrieved 30 October 2014.
- Gordon, Lawrence; Loeb, Martin (26 September 2011). "You May Be Fighting the Wrong Security Battles". The Wall Street Journal. Retrieved 9 May 2014.
- Palin, Adam (30 May 2013). "Maryland professors weigh up cyber risks". Financial Times. Retrieved 9 May 2014.