Generalised logistic function

The generalised (generalized) logistic function or curve, also known as Richards' curve, originally developed for growth modelling, is an extension of the logistic or sigmoid functions, allowing for more flexible S-shaped curves:

${\displaystyle Y(t)=A+{K-A \over (C+Qe^{-Bt})^{1/\nu }}}$

A=0, K=1, B=3, Q=ν=0.5, M=0, C=1

Effect of varying parameter A. All other parameters are 1.

Effect of varying parameter B. A = 0, all other parameters are 1.

Effect of varying parameter C. A = 0, all other parameters are 1.

Effect of varying parameter K. A = 0, all other parameters are 1.

Effect of varying parameter Q. A = 0, all other parameters are 1.

Effect of varying parameter ${\displaystyle \nu }$. A = 0, all other parameters are 1.

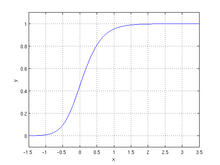
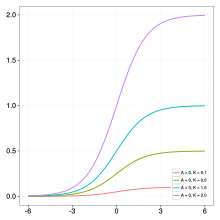
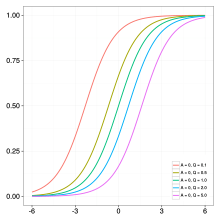
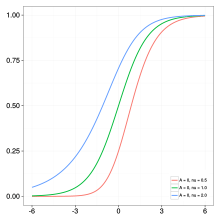
where ${\displaystyle Y}$ = weight, height, size etc., and ${\displaystyle t}$ = time.

It has five parameters:

• ${\displaystyle A}$: the lower asymptote;
• ${\displaystyle K}$: the upper asymptote when ${\displaystyle C=1}$. If ${\displaystyle A=0}$ and ${\displaystyle C=1}$ then ${\displaystyle K}$ is called the carrying capacity;
• ${\displaystyle B}$: the growth rate;
• ${\displaystyle \nu >0}$ : affects near which asymptote maximum growth occurs.
• ${\displaystyle Q}$: is related to the value ${\displaystyle Y(0)}$
• ${\displaystyle C}$: typically takes a value of 1. Otherwise, the upper asymptote is ${\displaystyle A+{K-A \over {\sqrt[{\nu }]{C}}}}$

The equation can also be written:

${\displaystyle Y(t)=A+{K-A \over (C+e^{-B(t-M)})^{1/\nu }}}$

where ${\displaystyle M}$ can be thought of as a starting time, ${\displaystyle t_{0}}$ (at which ${\displaystyle Y(t_{0})=A+{K-A \over (C+1)^{1/\nu }}}$ )

Including both ${\displaystyle Q}$ and ${\displaystyle M}$ can be convenient:

${\displaystyle Y(t)=A+{K-A \over (C+Qe^{-B(t-M)})^{1/\nu }}}$

this representation simplifies the setting of both a starting time and the value of Y at that time.

The general model is sometimes named a "Richards' curve" after F. J. Richards, who proposed the general form for the family of models in 1959.

The logistic, with maximum growth rate at time ${\displaystyle M}$, is the case where ${\displaystyle Q=\nu =1}$.

Generalised logistic differential equation

A particular case of the generalised logistic function is:

${\displaystyle Y(t)={K \over (1+Qe^{-\alpha \nu (t-t_{0})})^{1/\nu }}}$

which is the solution of the Richards' differential equation (RDE):

${\displaystyle Y^{\prime }(t)=\alpha \left(1-\left({\frac {Y}{K}}\right)^{\nu }\right)Y}$

with initial condition

${\displaystyle Y(t_{0})=Y_{0}}$

where

${\displaystyle Q=-1+\left({\frac {K}{Y_{0}}}\right)^{\nu }}$

provided that ν > 0 and α > 0.

The classical logistic differential equation is a particular case of the above equation, with ν =1, whereas the Gompertz curve can be recovered in the limit ${\displaystyle \nu \rightarrow 0^{+}}$ provided that:

${\displaystyle \alpha =O\left({\frac {1}{\nu }}\right)}$

In fact, for small ν it is

${\displaystyle Y^{\prime }(t)=Yr{\frac {1-\exp \left(\nu \ln \left({\frac {Y}{K}}\right)\right)}{\nu }}\approx rY\ln \left({\frac {Y}{K}}\right)}$

The RDE models many growth phenomena, including the growth of tumours. In oncology its main biological features are similar to those of the Logistic curve model.

The RDE models are widely used to describe infection trajectory in epidemiological modeling; see for COVID-19 application.

Gradient of generalized logistic function

When estimating parameters from data, it is often necessary to compute the partial derivatives of the logistic function with respect to parameters at a given data point ${\displaystyle t}$ (see [1]). For the case where ${\displaystyle C=1}$,

${\displaystyle {\begin{aligned}\\{\frac {\partial Y}{\partial A}}&=1-(1+Qe^{-B(t-M)})^{-1/\nu }\\\\{\frac {\partial Y}{\partial K}}&=(1+Qe^{-B(t-M)})^{-1/\nu }\\\\{\frac {\partial Y}{\partial B}}&={\frac {(K-A)(t-M)Qe^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\\{\frac {\partial Y}{\partial \nu }}&={\frac {(K-A)\ln(1+Qe^{-B(t-M)})}{\nu ^{2}(1+Qe^{-B(t-M)})^{\frac {1}{\nu }}}}\\\\{\frac {\partial Y}{\partial Q}}&=-{\frac {(K-A)e^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\\{\frac {\partial Y}{\partial M}}&=-{\frac {(K-A)QBe^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\end{aligned}}}$

Application to COVID-19 epidemiological modeling

Role of the shape parameter ${\displaystyle \xi }$ in the generalized logistic function

Roles of the three parameters in the generalized logistic function

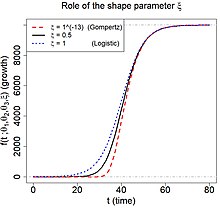
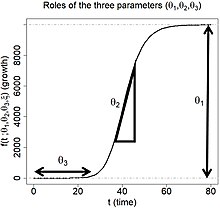
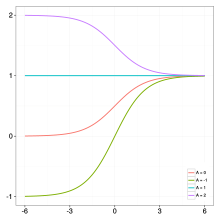
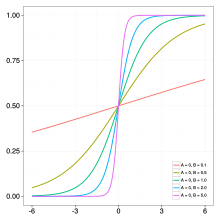
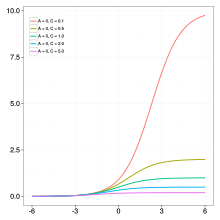
Generalized logistic function (Richards growth curve) is widely used in modelling COVID-19 infection trajectories [2]. Infection trajectory is a (typically daily) time series data for the cumulative number of infected cases for a subject. Subject can be certain country, city, state, etc. There are variant re-parameterizations in the literature, and one of frequently used forms is

${\displaystyle f(t;\theta _{1},\theta _{2},\theta _{3},\xi )=\theta _{1}\cdot [1+\xi \cdot \exp\{-\theta _{2}\cdot (t-\theta _{3})\}]^{-1/\xi }}$

where ${\displaystyle \theta _{1},\theta _{2},\theta _{3}}$ are real numbers, and ${\displaystyle \xi }$ is a positive real number. The flexibility of the curve ${\displaystyle f}$ is due to the parameter ${\displaystyle \xi }$: (i) if ${\displaystyle \xi =1}$ then the curve reduces to the logistic function, and (ii) if ${\displaystyle \xi }$ converges to zero, then the curve coverges to the Gompertz function. In epidemiological modeling, the parameters ${\displaystyle \theta _{1}}$, ${\displaystyle \theta _{2}}$, and ${\displaystyle \theta _{3}}$ represent the final epidemic size, infection rate, and lag phase, respectively. See the right panels for pictorial description of an examplary infection trajectory when ${\displaystyle (\theta _{1},\theta _{2},\theta _{3})}$ are designated by ${\displaystyle (10,000,0.2,40)}$ while varying the ${\displaystyle \xi }$ to be ${\displaystyle 1\times 10^{-13}\approx 0}$, ${\displaystyle 0.5}$, and ${\displaystyle 1}$, respectively.

Special cases

The following functions are specific cases of Richards' curves:

• Logistic function
• Gompertz curve
• Von Bertalanffy function
• Monomolecular curve

Footnotes

1. Fekedulegn, Desta; Mairitin P. Mac Siurtain; Jim J. Colbert (1999). "Parameter Estimation of Nonlinear Growth Models in Forestry" (PDF). Silva Fennica. 33 (4): 327–336. Archived from the original (PDF) on 2011-09-29. Retrieved 2011-05-31.
2. Lee, Se Yoon; Lei, Bowen; Mallick, Bani (2020). "Estimation of COVID-19 spread curves integrating global data and borrowing information". PLOS ONE. doi:10.1371/journal.pone.0236860.

References

• Richards, F. J. (1959). "A Flexible Growth Function for Empirical Use". Journal of Experimental Botany. 10 (2): 290–300. doi:10.1093/jxb/10.2.290.
• Pella, J. S.; Tomlinson, P. K. (1969). "A Generalised Stock-Production Model". Bull. Inter-Am. Trop. Tuna Comm. 13: 421–496.
• Lei, Y. C.; Zhang, S. Y. (2004). "Features and Partial Derivatives of Bertalanffy–Richards Growth Model in Forestry". Nonlinear Analysis: Modelling and Control. 9 (1): 65–73.
• Lee, Se Yoon; Lei, Bowen; Mallick, Bani (2020). "Estimation of COVID-19 spread curves integrating global data and borrowing information". PLOS ONE. doi:10.1371/journal.pone.0236860.