Game classification
Game classification is the classification of games, forming a game taxonomy. Many different methods of classifying games exist.
Physical education
There are four basic approaches to classifying the games used in physical education:[1]
- Game categories
- This is a classification scheme proposed by Nicols, who classifies games according to three major categories: the game's physical requirements (i.e. what the game requires in addition to the players — equipment, size and nature of playing field, and so forth), the structure of the game (i.e. number of players, groupings of players, strategies, and so forth), and the game's personal requirements (i.e. what the game requires of the player — motor skills, fitness levels, numeracy, social skills, and so forth).
- Games for understanding
- This is a classification scheme proposed by Werner and Alomond that classifies games according to their strategies. It divides games into target games (e.g. archery); net or wall games (e.g. tennis); striking and field games (e.g. cricket); and invasion games (e.g. football).
- Core content
- This is a classification scheme proposed by Allison and Barrett[2] that categorizes games by their form (i.e. whether they are novel games proposed by the teacher or children, or whether they are existing games already widely played), by the movement skills that they require, by the "movement concepts" and game tactics that they require, and by the educational results of the game.
- Developmental games
- This is a classification scheme proposed by Gallahue and Celand that classifies games into four developmental levels, as part of an overall educational strategy of applying, reinforcing, and implementing movement and sports skills. The levels, in ascending order, are "low-level", "complex", "lead-up", and "official sports".
Video games
There are several methods of classifying video games.
Solomon[3] puts forward a "commonsense, but broad" classification of video games, into simulations (the game reflects reality), abstract games (the game itself is the focus of interest), and sports. In addition to these he points out that games (in general, not just video games) fall into classes according to numbers of players. Games with two players encompass board games such as chess. Games with multiple players encompass card games such as poker, and marketed family games such as Monopoly and Scrabble. Puzzles and Solitaire are one-player games. He also includes zero-player games, such as Conway's Game of Life, although acknowledging that others argue that such games do not constitute a game, because they lack any element of competition. He asserts that such zero-player games are nonetheless games because they are used recreationally.
Another method, developed by Wright, divides games into the following categories: educational or informative, sports, sensorimotor (e.g. action games, video games, fighting and shoot 'em up games, and driving and racing simulators), other vehicular simulators (not covered by driving and racing), strategy games (e.g. adventure games, war games, strategic simulations, role-playing games, and puzzles), and "other".[4]
A third method, developed by Funk and Buchman, and refined by others, classifies electronic games into six categories: general entertainment (no fighting or destruction), educational (learning or problem solving), fantasy violence (cartoon characters that must fight or destroy things, and risk being killed, in order to achieve a goal), human violence (like fantasy violence, but with human rather than cartoon characters), nonviolent sports (no fighting or destruction), and sports violence (fighting or destruction involved).[4]
Classification by causes of uncertainty
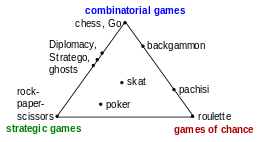
Games can be categorized by the source of uncertainty which confront the players:[5][6]
- Chance
- Combinatorics (the large number of sequences of moves)
- Different states of information among the players (each player knows only his own cards)
Based on these three causes three classes of games arise:
- Games of chance
- Combinatorial games
- Games of bluffing and strategy
Game theory
Game theory classifies games according to several criteria: whether a game is a symmetric game or an asymmetric one, what a game's "sum" is (zero-sum, constant sum, and so forth), whether a game is a sequential game or a simultaneous one, whether a game comprises perfect information or imperfect information, and whether a game is determinate.
See also
| Wikimedia Commons has media related to Game. |
- Entertainment Software Rating Board
- Video game genre
- Game of skill and Game of chance — another classification scheme
References
- David P. Swain; David L. Gallahue; Frances Cleland Donnelly (2003). Developmental Physical Education for Today's Children. Human Kinetics. pp. 571–573. ISBN 0-7360-3388-2.
- Rink J. (2001). Investigating the Assumptions of Pedagogy in Journal of Teaching in Physical Education. Human Kinetics Publishers Inc. pp. 112–128 Vol 20, No. 2.
- Eric Solomon (1984). Games Programming. Cambridge University Press. pp. 10–11. ISBN 0-521-27110-X.
- Victor C. Strasburger and Barbara J. Wilson (2002). Children, Adolescents and the Media. Sage Publications. pp. 122–123. ISBN 0-7619-2125-7.
- Jörg Bewersdorff (2004). Luck, Logic, and White Lies: The Mathematics of Games (PDF). AK Peters. p. xi. ISBN 1-56881-210-8.
- Hugo Kastner (January 2014). "100 Highlight among games" (PDF). WIN the Games Journal. 38 (460): 36–37. ISSN 0257-361X.
Further reading
- Tim Hopper; Rick Bell. "Games classification system: Teaching strategic understanding and tactical awareness" (PDF). Cahperd. 66 (4): 14–19.
- David Bunker; Rod Thorpe; Peter Werner (1996). "Teaching Games for Understanding: Evolution of a Model" (PDF). The Journal of Physical Education, Recreation & Dance. 67. Archived from the original on 2004-03-10.
- Lindley, C. A. (3 October 2003). "Game Taxonomies: A High Level Framework for Game Analysis and Design". Gamasutra.
- Sebastian Pape; Laura Dietz; Peter Tandler (2 April 2004). "Single Display Gaming: Examining Collaborative Games for Multi-User Tabletops" (PDF). Fraunhofer Integrated Publication and Information Systems Institute. Archived from the original (PDF) on 2007-06-26. Cite journal requires
|journal=(help) - Amund Tveit; Gisle B. Tveit (2002). "Game Usage Mining: Information Gathering for Knowledge Discovery in Massive Multiplayer Games" (PDF). Archived from the original (PDF) on 2003-10-05. Cite journal requires
|journal=(help) - Maja Pivec; Anni Koubek; Claudio Dondi (2004). Guidelines for Game-Based Learning. Pabst Science Publishers. pp. 54–57. ISBN 1-59326-072-5.
- Deborah P. Vossen (21 April 2004). "The Nature and Classification of Games" (PDF). 10 (1): 75–77. Archived from the original (PDF) on 2009-04-24. Cite journal requires
|journal=(help)