Fuzzy extractor

Fuzzy extractors are a method that allows biometric data to be used as inputs to standard cryptographic techniques for security. "Fuzzy", in this context, refers to the fact that the fixed values required for cryptography will be extracted from values close to but not identical to the original key, without compromising the security required. One application is to encrypt and authenticate users records, using the biometric inputs of the user as a key.

Fuzzy extractors are a biometric tool that allows for user authentication, using a biometric template constructed from the user's biometric data as the key. They extract a uniform and random string ${\displaystyle R}$ from an input ${\displaystyle w}$ with a tolerance for noise. If the input changes to ${\displaystyle w'}$ but is still close to ${\displaystyle w}$, the same string ${\displaystyle R}$ will be re-constructed. To achieve this, during the initial computation of ${\displaystyle R}$ the process also outputs a helper string ${\displaystyle P}$which will be stored to recover ${\displaystyle R}$ later and can be made public without compromising the security of ${\displaystyle R}$. The security of the process is ensured also when an adversary modifies ${\displaystyle P}$. Once the fixed string ${\displaystyle R}$ has been calculated, it can be used for example for key agreement between a user and a server based only on a biometric input.

Historically, the first biometric system of this kind was designed by Juels and Wattenberg and was called "Fuzzy commitment", where the cryptographic key is decommitted using biometric data. Later, Juels and Sudan came up with Fuzzy vault schemes which are order invariant for the fuzzy commitment scheme but uses a Reed–Solomon code. Codeword is evaluated by polynomial and the secret message is inserted as the coefficients of the polynomial. The polynomial is evaluated for different values of a set of features of the biometric data. So Fuzzy commitment and Fuzzy Vault were precursors to Fuzzy extractors.

This description is based on the papers "Fuzzy Extractors: A Brief Survey of Results from 2004 to 2006" and "Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data"[1] by Yevgeniy Dodis, Rafail Ostrovsky, Leonid Reyzin and Adam Smith

Motivation

In order for fuzzy extractors to generate strong keys from biometric and other noisy data, cryptography paradigms will be applied to this biometric data. This means they must be allowed to

(1) Limit the number of assumptions about the content of the biometric data (this data comes from a variety of sources, so in order to avoid exploitation by an adversary, it's best to assume the input is unpredictable)

(2) Apply usual cryptographic techniques to the input. (Fuzzy extractors convert biometric data into secret, uniformly random and reliably reproducible random strings).

These techniques can also have other broader applications for other type of noisy inputs such as approximative data from human memory, images used as passwords, keys from quantum channel.[1] According to the Differential Privacy paper by Cynthia Dwork (ICALP 2006), fuzzy extractors also have applications in the proof of impossibility of the strong notions of privacy for statistical databases.

Basic definitions

Predictability

Predictability indicates the probability that an adversary can guess a secret key. Mathematically speaking, the predictability of a random variable ${\displaystyle A}$ is ${\displaystyle \max _{\mathrm {a} }P[A=a]}$.

For example, given a pair of random variable ${\displaystyle A}$ and ${\displaystyle B}$, if the adversary knows ${\displaystyle b}$ of ${\displaystyle B}$, then the predictability of ${\displaystyle A}$ will be ${\displaystyle \max _{\mathrm {a} }P[A=a|B=b]}$. So, an adversary can predict ${\displaystyle A}$ with ${\displaystyle E_{b\leftarrow B}[\max _{\mathrm {a} }P[A=a|B=b]]}$. We use the average over ${\displaystyle B}$ as it is not under adversary control, but since knowing ${\displaystyle b}$ makes the prediction of ${\displaystyle A}$ adversarial, we take the worst case over ${\displaystyle A}$.

Min-entropy

Min-entropy indicates the worst-case entropy. Mathematically speaking, it is defined as ${\displaystyle H_{\infty }(A)=-\log(\max _{\mathrm {a} }P[A=a])}$ .

A random variable with a min-entropy at least of ${\displaystyle m}$ is called a ${\displaystyle m}$-source.

Statistical distance

Statistical distance is a measure of distinguishability. Mathematically speaking, it is expressed for two probability distributions ${\displaystyle A}$ and ${\displaystyle B}$ as ${\displaystyle SD[A,B]}$ = ${\displaystyle {\frac {1}{2}}\sum _{\mathrm {v} }|P[A=v]-P[B=v]|}$. In any system, if ${\displaystyle A}$ is replaced by ${\displaystyle B}$, it will behave as the original system with a probability at least of ${\displaystyle 1-SD[A,B]}$.

Definition 1 (strong extractor)

Setting ${\displaystyle M}$ as a strong randomness extractor. The randomized function Ext: ${\displaystyle M\rightarrow \{0,1\}^{l}}$ with randomness of length ${\displaystyle r}$ is a ${\displaystyle (m,l,\epsilon )}$ strong extractor if for all ${\displaystyle m}$-sources ${\displaystyle W}$ on ${\displaystyle M(Ext(W;I),I)\approx _{\epsilon }(U_{l},U_{r}),}$ where ${\displaystyle I=U_{r}}$ is independent of ${\displaystyle W}$.

The output of the extractor is a key generated from ${\displaystyle w\leftarrow W}$ with the seed ${\displaystyle i\leftarrow I}$. It behaves independently of other parts of the system with the probability of ${\displaystyle 1-\epsilon }$. Strong extractors can extract at most ${\displaystyle l=m-2log{\frac {1}{\epsilon }}+O(1)}$ bits from an arbitrary ${\displaystyle m}$-source.

Secure sketch

Secure sketch makes it possible to reconstruct noisy input, so that if the input is ${\displaystyle w}$ and the sketch is ${\displaystyle s}$, given ${\displaystyle s}$ and a value ${\displaystyle w'}$close to ${\displaystyle w}$, ${\displaystyle w}$ can be recovered. But the sketch ${\displaystyle s}$ must not reveal information about ${\displaystyle w}$, in order to keep it secure.

If ${\displaystyle \mathbb {M} }$ is a metric space with the distance function dis, Secure sketch recovers the string ${\displaystyle w\in \mathbb {M} }$ from any close string ${\displaystyle w'\in \mathbb {M} }$ without disclosing ${\displaystyle w}$.

Definition 2 (secure sketch)

An ${\displaystyle (m,{\tilde {m}},t)}$ secure sketch is a pair of efficient randomized procedures (the Sketch noted SS, the Recover noted Rec) such that :

(1) The sketching procedure SS applied on input ${\displaystyle w\in \mathbb {M} }$ returns a string ${\displaystyle s\in {\{0,1\}^{*}}}$.

The recovery procedure Rec uses as input two elements ${\displaystyle w'\in \mathbb {M} }$ and ${\displaystyle s\in {\{0,1\}^{*}}}$.

(2) Correctness: If ${\displaystyle dis(w,w')\leq t}$ then ${\displaystyle Rec(w',SS(w))=w}$.

(3) Security: For any ${\displaystyle m}$-source over ${\displaystyle M}$, the min-entropy of ${\displaystyle W}$ given ${\displaystyle s}$ is high:

for any ${\displaystyle (W,E)}$, if ${\displaystyle {\tilde {H}}_{\mathrm {\infty } }(W|E)\geq m}$, then ${\displaystyle {\tilde {H}}_{\mathrm {\infty } }(W|SS(W),E)\geq {\tilde {m}}}$.

Fuzzy extractor

Fuzzy extractors do not recover the original input but generate a string ${\displaystyle R}$ (which is close to uniform) from ${\displaystyle w}$ and allow its subsequent reproduction (using helper string ${\displaystyle P}$) given any ${\displaystyle w'}$ close to ${\displaystyle w}$. Strong extractors are a special case of fuzzy extractors when ${\displaystyle t}$ = 0 and ${\displaystyle P=I}$.

Definition 3 (fuzzy extractor)

An ${\displaystyle (m,l,t,\epsilon )}$ fuzzy extractor is a pair of efficient randomized procedures (Gen – Generate and Rep – Reproduce) such that:

(1) Gen, given ${\displaystyle w\in \mathbb {M} }$, outputs an extracted string ${\displaystyle R\in {\mathbb {\{} 0,1\}^{l}}}$ and a helper string ${\displaystyle P\in {\mathbb {\{} 0,1\}^{*}}}$.

(2) Correctness: If ${\displaystyle dis(w,w')\leq t}$ and ${\displaystyle (R,P)\leftarrow Gen(w)}$, then ${\displaystyle Rep(w',P)=R}$.

(3) Security: For all m-sources ${\displaystyle W}$ over ${\displaystyle M}$, the string ${\displaystyle R}$ is nearly uniform even given ${\displaystyle P}$, So ${\displaystyle {\tilde {H}}_{\mathrm {\infty } }(W|E)\geq m}$, then ${\displaystyle (R,P,E)\approx (U_{\mathrm {l} },P,E)}$.

So Fuzzy extractors output almost uniform random sequences of bits which are a prerequisite for using cryptographic applications (as secret keys). Since the output bits are slightly non-uniform, there's a risk of a decreased security, but the distance from a uniform distribution is no more than ${\displaystyle \epsilon }$ and as long as this distance is sufficiently small, the security will remain adequate.

Secure sketches and fuzzy extractors

Secure sketches can be used to construct fuzzy extractors. Like applying SS to ${\displaystyle w}$ to obtain ${\displaystyle s}$ and strong extractor Ext with randomness ${\displaystyle x}$ to ${\displaystyle w}$ to get ${\displaystyle R}$. ${\displaystyle (s,x)}$ can be stored as helper string ${\displaystyle P}$. ${\displaystyle R}$ can be reproduced by ${\displaystyle w'}$ and ${\displaystyle P=(s,x)}$. ${\displaystyle Rec(w',s)}$ can recover ${\displaystyle w}$ and ${\displaystyle Ext(w,x)}$ can reproduce ${\displaystyle R}$. The following lemma formalizes this.

Lemma 1 (fuzzy extractors from sketches)

Assume (SS,Rec) is an ${\displaystyle (M,m,{\tilde {m}},t)}$ secure sketch and let Ext be an average-case ${\displaystyle (n,{\tilde {m}},l,\epsilon )}$ strong extractor. Then the following (Gen, Rep) is an ${\displaystyle (M,m,l,t,\epsilon )}$ fuzzy extractor: (1) Gen ${\displaystyle (w,r,x)}$: set ${\displaystyle P=(SS(w;r),x),R=Ext(w;x),}$ and output ${\displaystyle (R,P)}$. (2) Rep ${\displaystyle (w',(s,x))}$: recover ${\displaystyle w=Rec(w',s)}$ and output ${\displaystyle R=Ext(w;x)}$.

Proof: From the definition of secure sketch (Definition 2), ${\displaystyle H_{\infty }(W|SS(W))\geq {\tilde {m}}}$. And since Ext is an average-case ${\displaystyle (n,m,l,\epsilon )}$-strong extractor. ${\displaystyle SD((Ext(W;X),SS(W),X),(U_{l},SS(W),X))=SD((R,P),(U_{l},P))\leq \epsilon .}$

Corollary 1

If (SS,Rec) is an ${\displaystyle (M,m,{\tilde {m}},t)}$ secure sketch and Ext is an ${\displaystyle (n,{\tilde {m}}-log({\frac {1}{\delta }}),l,\epsilon )}$ strong extractor, then the above construction (Gen,Rep) is a ${\displaystyle (M,m,l,t,\epsilon +\delta )}$ fuzzy extractor.

The reference paper includes many generic combinatorial bounds on secure sketches and fuzzy extractors.[1]

Basic constructions

Due to their error tolerant properties, a secure sketches can be treated, analyzed, and constructed like a ${\displaystyle (n,k,d)_{\mathcal {F}}}$ general error correcting code or ${\displaystyle [n,k,d]_{\mathcal {F}}}$ for linear codes, where ${\displaystyle n}$ is the length of codewords, ${\displaystyle k}$ is the length of the message to be codded, ${\displaystyle d}$ is the distance between codewords, and ${\displaystyle {\mathcal {F}}}$ is the alphabet. If ${\displaystyle {\mathcal {F}}^{n}}$ is the universe of possible words then it may be possible to find an error correcting code ${\displaystyle C\in {\mathcal {F}}^{n}}$ that has a unique codeword ${\displaystyle c\in C}$ for every ${\displaystyle w\in {\mathcal {F}}^{n}}$ and have a Hamming distance of ${\displaystyle dis_{Ham}(c,w)\leq (d-1)/2}$. The first step for constructing a secure sketch is determining the type of errors that will likely occur and then choosing a distance to measure.

Red is the code-offset construction, blue is the syndrome construction, green represents edit distance and other complex constructions.

Hamming distance constructions

When there is no risk of data being deleted and only of it being corrupted then the best measurement to use for error correction is the Hamming distance. There are two common constructions for correcting Hamming errors depending on whether the code is linear or not. Both constructions start with an error correcting code that has a distance of ${\displaystyle 2t+1}$ where ${\displaystyle {t}}$ is the number of tolerated errors.

Code-offset construction

When using a ${\displaystyle (n,k,2t+1)_{\mathcal {F}}}$ general code, assign a uniformly random codeword ${\displaystyle c\in C}$ to each ${\displaystyle w}$, then let ${\displaystyle SS(w)=s=w-c}$ which is the shift needed to change ${\displaystyle c}$ into ${\displaystyle w}$. To fix errors in ${\displaystyle w'}$ subtract ${\displaystyle s}$ from ${\displaystyle w'}$ then correct the errors in the resulting incorrect codeword to get ${\displaystyle c}$ and finally add ${\displaystyle s}$ to ${\displaystyle c}$ to get ${\displaystyle w}$. This means ${\displaystyle Rec(w',s)=s+dec(w'-s)=w}$. This construction can achieve the best possible tradeoff between error tolerance and entropy loss when ${\displaystyle {\mathcal {F}}\geq n}$ and a Reed–Solomon code is used resulting in an entropy loss of ${\displaystyle 2t\log({\mathcal {F}})}$. The only way to improve upon would be to find a code better than Reed–Solomon.

Syndrome construction

When using a ${\displaystyle [n,k,2t+1]_{\mathcal {F}}}$ linear code let the ${\displaystyle SS(w)=s}$ be the syndrome of ${\displaystyle w}$. To correct ${\displaystyle w'}$ find a vector ${\displaystyle e}$ such that ${\displaystyle syn(e)=syn(w')-s}$, then ${\displaystyle w=w'-e}$.

Set difference constructions

When working with a very large alphabet or very long strings resulting in a very large universe ${\displaystyle {\mathcal {U}}}$, it may be more efficient to treat ${\displaystyle w}$ and ${\displaystyle w'}$ as sets and look at set differences to correct errors. To work with a large set ${\displaystyle w}$ it is useful to look at its characteristic vector ${\displaystyle x_{w}}$, which is a binary vector of length ${\displaystyle n}$ that has a value of 1 when an element ${\displaystyle a\in {\mathcal {U}}}$ and ${\displaystyle a\in w}$, or 0 when ${\displaystyle a\notin w}$. The best way to decrease the size of a secure sketch when ${\displaystyle n}$ is large is make ${\displaystyle k}$ large since the size is determined by ${\displaystyle n-k}$. A good code to base this construction on is a ${\displaystyle [n,n-t\alpha ,2t+1]_{2}}$ BCH code where ${\displaystyle n=2^{\alpha }-1}$ and ${\displaystyle t\ll n}$ so ${\displaystyle k\leq n-log{n \choose {t}}}$, it is also useful that BCH codes can be decode in sub-linear time.

Pin sketch construction

Let ${\displaystyle SS(w)=s=syn(x_{w})}$. To correct ${\displaystyle w'}$ first find ${\displaystyle SS(w')=s'=syn(x_{w}')}$, then find a set v where ${\displaystyle syn(x_{v})=s'-s}$, finally compute the symmetric difference to get ${\displaystyle Rec(w',s)=w'\triangle v=w}$. While this is not the only construction than can be used to set the difference, it is the easiest one.

Edit distance constructions

When data can be corrupted or deleted, the best measurement to use is edit distance. To make a construction based on edit distance, the easiest is to start with a construction for set difference or hamming distance as an intermediate correction step and then build the edit distance construction around that.

Other distance measure constructions

There are many other types of errors and distances that can be used to model other situations. Most of these other possible constructions are built upon simpler constructions, like edit distance constructions.

Improving error-tolerance via relaxed notions of correctness

It can be shown that the error-tolerance of a secure sketch can be improved by applying a probabilistic method to error correction and only requesting errors to be correctable with a high probability. This allows to exceed the Plotkin bound which limits to correcting ${\displaystyle n/4}$ errors, and to approach Shannon’s bound allowing for nearly ${\displaystyle n/2}$ corrections. To achieve this enhanced error correction, a less restrictive error distribution model must be used.

Random errors

For this most restrictive model use a BSC${\displaystyle _{p}}$ to create a ${\displaystyle w'}$ that a probability ${\displaystyle p}$ at each position in ${\displaystyle w'}$ that the bit received is wrong. This model can show that entropy loss is limited to ${\displaystyle nH(p)-o(n)}$, where ${\displaystyle H}$ is the binary entropy function, and if min-entropy ${\displaystyle m\geq n(H({\frac {1}{2}}-\gamma ))+\varepsilon }$ then ${\displaystyle n({\frac {1}{2}}-\gamma )}$ errors can be tolerated, for some constant ${\displaystyle \gamma >0}$.

Input-dependent errors

For this model errors do not have a known distribution and can be from an adversary, the only constraints are ${\displaystyle dis_{\text{err}}\leq t}$ and that a corrupted word depends only on the input ${\displaystyle w}$ and not on the secure sketch. It can be shown for this error model that there will never be more than ${\displaystyle t}$ errors since this model can account for all complex noise processes, meaning that Shannon’s bound can be reached, to do this a random permutation is prepended to the secure sketch that will reduce entropy loss.

Computationally bounded errors

This differs from the input dependent model by having errors that depend on both the input ${\displaystyle w}$ and the secure sketch, and an adversary is limited to polynomial time algorithms for introducing errors. Since algorithms that can run in better than polynomial time are not currently feasible in the real world, then a positive result using this error model would guarantee that any errors can be fixed. This is the least restrictive model the only known way to approach Shannon’s bound is to use list-decodable codes although this may not always be useful in practice since returning a list instead of a single codeword may not always be acceptable.

Privacy guarantees

In general a secure system attempts to leak as little information as possible to an adversary. In the case of biometrics if information about the biometric reading is leaked the adversary may be able to learn personal information about a user. For example an adversary notices that there is a certain pattern in the helper strings that implies the ethnicity of the user. We can consider this additional information a function ${\displaystyle f(W)}$. If an adversary were to learn a helper string, it must be ensured that, from this data he can not infer any data about the person from which the biometric reading was taken.

Correlation between helper string and biometric input

Ideally the helper string ${\displaystyle P}$ would reveal no information about the biometric input ${\displaystyle w}$. This is only possible when every subsequent biometric reading ${\displaystyle w'}$ is identical to the original ${\displaystyle w}$. In this case there is actually no need for the helper string, so it is easy to generate a string that is in no way correlated to ${\displaystyle w}$.

Since it is desirable to accept biometric input ${\displaystyle w'}$ similar to ${\displaystyle w}$ the helper string ${\displaystyle P}$ must be somehow correlated. The more different ${\displaystyle w}$ and ${\displaystyle w'}$ are allowed to be, the more correlation there will be between ${\displaystyle P}$ and ${\displaystyle w}$, the more correlated they are the more information ${\displaystyle P}$ reveals about ${\displaystyle w}$. We can consider this information to be a function ${\displaystyle f(W)}$. The best possible solution is to make sure the adversary can't learn anything useful from the helper string.

Gen(W) as a probabilistic map

A probabilistic map ${\displaystyle Y()}$ hides the results of functions with a small amount of leakage ${\displaystyle \epsilon }$. The leakage is the difference in probability two adversaries have of guessing some function when one knows the probabilistic map and one does not. Formally:

${\displaystyle |Pr[A_{1}(Y(W))=f(W)]-Pr[A_{2}()=f(W)]|\leq \epsilon }$

If the function ${\displaystyle Gen(W)}$ is a probabilistic map, then even if an adversary knows both the helper string ${\displaystyle P}$ and the secret string ${\displaystyle R}$ they are only negligibly more likely figure something out about the subject as if they knew nothing. The string ${\displaystyle R}$ is supposed to kept secret, so even if it is leaked (which should be very unlikely) the adversary can still figure out nothing useful about the subject, as long as ${\displaystyle \epsilon }$ is small. We can consider ${\displaystyle f(W)}$ to be any correlation between the biometric input and some physical characteristic of the person. Setting ${\displaystyle Y=Gen(W)=R,P}$ in the above equation changes it to:

${\displaystyle |\Pr[A_{1}(R,P)=f(W)]-\Pr[A_{2}()=f(W)]|\leq \epsilon }$

This means that if one adversary ${\displaystyle A_{1}}$ has ${\displaystyle (R,P)}$ and a second adversary ${\displaystyle A_{2}}$ knows nothing, their best guesses at ${\displaystyle f(W)}$ are only ${\displaystyle \epsilon }$ apart.

Uniform fuzzy extractors

Uniform fuzzy extractors are a special case of fuzzy extractors, where the output ${\displaystyle (R,P)}$ of ${\displaystyle Gen(W)}$ are negligibly different from strings picked from the uniform distribution, i.e. ${\displaystyle (R,P)\approx _{\epsilon }(U_{\ell },U_{|P|})}$

Uniform secure sketches

Since secure sketches imply fuzzy extractors, constructing a uniform secure sketch allows for the easy construction of a uniform fuzzy extractor. In a uniform secure sketch the sketch procedure ${\displaystyle SS(w)}$ is a randomness extractor ${\displaystyle Ext(w;i)}$. Where ${\displaystyle w}$ is the biometric input and ${\displaystyle i}$ is the random seed. Since randomness extractors output a string that appears to be from a uniform distribution they hide all the information about their input.

Applications

Extractor sketches can be used to construct ${\displaystyle (m,t,\epsilon )}$-fuzzy perfectly one-way hash functions. When used as a hash function the input ${\displaystyle w}$ is the object you want to hash. The ${\displaystyle P,R}$ that ${\displaystyle Gen(w)}$ outputs is the hash value. If one wanted to verify that a ${\displaystyle w'}$ within ${\displaystyle t}$ from the original ${\displaystyle w}$, they would verify that ${\displaystyle Rep(w',P)=R}$. ${\displaystyle (m,t,\epsilon )}$-fuzzy perfectly one-way hash functions are special hash functions where they accept any input with at most ${\displaystyle t}$ errors, compared to traditional hash functions which only accept when the input matches the original exactly. Traditional cryptographic hash functions attempt to guarantee that is it is computationally infeasible to find two different inputs that hash to the same value. Fuzzy perfectly one-way hash functions make an analogous claim. They make it computationally infeasible two find two inputs, that are more than ${\displaystyle t}$ Hamming distance apart and hash to the same value.

Protection against active attacks

An active attack could be one where the adversary can modify the helper string ${\displaystyle P}$. If the adversary is able to change ${\displaystyle P}$ to another string that is also acceptable to the reproduce function ${\displaystyle Rep(W,P)}$, it causes ${\displaystyle Rep(W,P)}$ to output an incorrect secret string ${\displaystyle {\tilde {R}}}$. Robust fuzzy extractors solve this problem by allowing the reproduce function to fail, if a modified helper string is provided as input.

Robust fuzzy extractors

One method of constructing robust fuzzy extractors is to use hash functions. This construction requires two hash functions ${\displaystyle H_{1}}$ and ${\displaystyle H_{2}}$. The ${\displaystyle Gen(W)}$ functions produces the helper string ${\displaystyle P}$ by appending the output of a secure sketch ${\displaystyle s=SS(w)}$ to the hash of both the reading ${\displaystyle w}$ and secure sketch ${\displaystyle s}$. It generates the secret string ${\displaystyle R}$ by applying the second hash function to ${\displaystyle w}$ and ${\displaystyle s}$. Formally: ${\displaystyle Gen(w):s=SS(w),return:P=(s,H_{1}(w,s)),R=H_{2}(w,s)}$

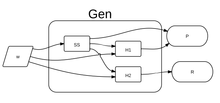
The reproduce function ${\displaystyle Rep(W,P)}$ also makes use of the hash functions ${\displaystyle H_{1}}$ and ${\displaystyle H_{2}}$. In addition to verifying the biometric input is similar enough to the one recovered using the ${\displaystyle Rec(W,S)}$ function, it also verifies that hash in the second part of ${\displaystyle P}$ was actually derived from ${\displaystyle w}$ and ${\displaystyle s}$. If both of those conditions are met it returns ${\displaystyle R}$ which is itself the second hash function applied to ${\displaystyle w}$ and ${\displaystyle s}$. Formally:

${\displaystyle Rep(w',{\tilde {P}}):}$ Get ${\displaystyle {\tilde {s}}}$ and ${\displaystyle {\tilde {h}}}$ from ${\displaystyle {\tilde {P}};{\tilde {w}}=Rec(w',{\tilde {s}}).}$ If ${\displaystyle \Delta ({\tilde {w}},w')\leq t}$ and ${\displaystyle {\tilde {h}}=H_{1}({\tilde {w}},{\tilde {s}})}$ then ${\displaystyle return:H_{2}({\tilde {w}},{\tilde {s}})}$ else ${\displaystyle return:fail}$

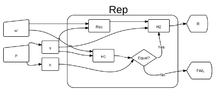
If ${\displaystyle P}$ has been tampered with it will be obvious because, ${\displaystyle Rep}$ will output fail with very high probability. To cause the algorithm accept a different ${\displaystyle P}$ an adversary would have to find a ${\displaystyle {\tilde {w}}}$ such that ${\displaystyle H_{1}(w,s)=H_{1}({\tilde {w}},{\tilde {s}})}$. Since hash function are believed to be one-way functions, it is computationally infeasible to find such a ${\displaystyle {\tilde {w}}}$. Seeing ${\displaystyle P}$ would provide the adversary with no useful information. Since, again, hash function are one-way functions, it is computationally infeasible for the adversary to reverse the hash function and figure out ${\displaystyle w}$. Part of ${\displaystyle P}$ is the secure sketch, but by definition the sketch reveals negligible information about its input. Similarly seeing ${\displaystyle R}$(even though it should never see it) would provide the adversary with no useful information as the adversary wouldn't be able to reverse the hash function and see the biometric input.

References

1. Yevgeniy Dodis, Rafail Ostrovsky, Leonid Reyzin, and Adam Smith. "Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data". 2008.

• Fuzzy Extractors: A Brief Survey of Results from 2004 to 2006
• Biometric Fuzzy Extractor Scheme for Iris Templates
• A Fuzzy Vault Scheme