Fusion adaptive resonance theory

Fusion adaptive resonance theory (fusion ART)[1][2][3] is a generalization of self-organizing neural networks known as Adaptive Resonance Theory[4] for learning recognition categories (or cognitive codes) across multiple pattern channels. It unifies a number of neural network models, supports several learning paradigms, notably unsupervised learning, supervised learning, and reinforcement learning, and can be applied for domain knowledge integration, memory representation,[5] and modelling of high level cognition.

Overview

Fusion adaptive resonance theory models is a natural extension of the original adaptive resonance theory (ART)[4][6] models developed by Stephen Grossberg and Gail A. Carpenter from a single pattern field to multiple pattern channels. Whereas the original ART models perform unsupervised learning of recognition nodes in response to incoming input patterns, fusion ART learns multi-channel mappings simultaneously across multi-modal pattern channels in an online and incremental manner.

The learning model

Fusion ART employs a multi-channel architecture (as shown below), comprising a category field ${\displaystyle F_{2}}$ connected to a fixed number of (K) pattern channels or input fields ${\displaystyle F_{1}^{c1},\dots ,F_{1}^{cK}}$ through bidirectional conditionable pathways. The model unifies a number of network designs, most notably Adaptive Resonance Theory (ART), Adaptive Resonance Associative Map (ARAM)[7] and Fusion Architecture for Learning and COgNition (FALCON),[8] developed over the past decades for a wide range of functions and applications.

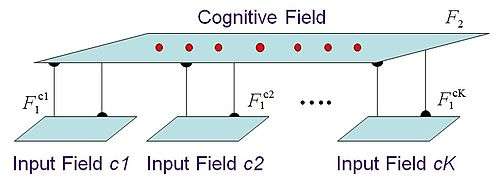
Given a set of multimodal patterns, each presented at a pattern channel, the fusion ART pattern encoding cycle comprises five key stages, namely code activation, code competition, activity readout, template matching, and template learning, as described below.

• Code activation: Given the input activity vectors ${\displaystyle {\vec {I}}^{ck}}$, one for each input field ${\displaystyle F_{1}^{ck}}$, the choice function ${\displaystyle T_{j}}$ of each ${\displaystyle F_{2}}$ node j is computed based on the combined overall similarity between the input patterns and the corresponding weight vectors ${\displaystyle {\vec {w}}_{j}^{ck}}$.
• Code competition: A code competition process follows under which the ${\displaystyle F_{2}}$ node with the highest choice function value is identified. The winner is indexed at J where ${\displaystyle T_{j}}$ is the maximum among all ${\displaystyle F_{2}}$ nodes. This indicates a winner-take-all strategy.
• Activity readout: During memory recall, the chosen ${\displaystyle F_{2}}$ node J performs a read out of its weight vectors to the input fields ${\displaystyle F_{1}^{ck}}$.
• Template matching: Before the activity readout is stabilized and node J can be used for learning, a template matching process checks that the weight templates of node J are sufficiently close to their respective input patterns. Specifically, resonance occurs if for each channel k, the match function of the chosen node J meets its vigilance criterion. If any of the vigilance constraints is violated, mismatch reset occurs in which the value of the choice function ${\displaystyle T_{J}}$ is set to 0 for the duration of the input presentation. Using a match tracking process, at the beginning of each input presentation, the vigilance parameter in each channel ck equals a baseline vigilance. When a mismatch reset occurs, the vigilance of all pattern channels are increased simultaneously until one of them is slightly larger than its corresponding match function, causing a reset. The search process then selects another ${\displaystyle F_{2}}$ node J under the revised vigilance criterion until a resonance is achieved.
• Template learning: Once a resonance occurs, for each channel ck, the weight vector ${\displaystyle {\vec {w}}_{J}^{ck}}$ is modified according to a learning rule which moves it towards the input pattern. When an uncommitted node is selected for learning, it becomes committed and a new uncommitted node is added to the ${\displaystyle F_{2}}$ field. Fusion ART thus expands its network architecture dynamically in response to the input patterns.

Types of fusion ART

The network dynamics described above can be used to support numerous learning operations. We show how fusion ART can be used for a variety of traditionally distinct learning tasks in the subsequent sections.

Original ART models

With a single pattern channel, the fusion ART architecture reduces to the original ART model. Using a selected vigilance value $\rho$, an ART model learns a set of recognition nodes in response to an incoming stream of input patterns in a continuous manner. Each recognition node in the ${\displaystyle F_{2}}$ field learns to encode a template pattern representing the key characteristics of a set of patterns. ART has been widely used in the context of unsupervised learning for discovering pattern groupings. Please refer to the selected ART literatures[4][6] for a review of ART's functionalities, interpretations, and applications.

Adaptive resonance associative map

By synchronizing pattern coding across multiple pattern channels, fusion ART learns to encode associative mappings across distinct pattern spaces. A specific instance of fusion ART with two pattern channels is known as adaptive resonance associative map (ARAM), that learns multi-dimensional supervised mappings from one pattern space to another pattern space. An ARAM system consists of an input field ${\displaystyle F_{1}^{a}}$, an output field ${\displaystyle F_{1}^{b}}$, and a category field ${\displaystyle F_{2}}$. Given a set of feature vectors presented at ${\displaystyle F_{1}^{a}}$ with their corresponding class vectors presented at ${\displaystyle F_{1}^{b}}$, ARAM learns a predictive model (encoded by the recognition nodes in ${\displaystyle F_{2}}$) that associates combinations of key features to their respective classes.

Fuzzy ARAM, based on fuzzy ART operations, has been successfully applied to numerous machine learning tasks, including personal profiling,[9] document classification,[10] personalized content management,[11] and DNA gene expression analysis.[12] In many benchmark experiments, ARAM has demonstrated predictive performance superior to those of many state-of-the-art machine learning systems, including C4.5, Backpropagation Neural Network, K Nearest Neighbour, and Support Vector Machines.

Fusion ART with domain knowledge

During learning, fusion ART formulates recognition categories of input patterns across multiple channels. The knowledge that fusion ART discovers during learning, is compatible with symbolic rule-based representation. Specifically, the recognition categories learned by the ${\displaystyle F_{2}}$ category nodes are compatible with a class of IF-THEN rules that maps a set of input attributes (antecedents) in one pattern channel to a disjoint set of output attributes (consequents) in another channel. Due to this compatibility, at any point of the incremental learning process, instructions in the form of IF-THEN rules can be readily translated into the recognition categories of a fusion ART system. The rules are conjunctive in the sense that the attributes in the IF clause and in the THEN clause have an AND relationship. Augmenting a fusion ART network with domain knowledge through explicit instructions serves to improve learning efficiency and predictive accuracy.

The fusion ART rule insertion strategy is similar to that used in Cascade ARTMAP, a generalization of ARTMAP that performs domain knowledge insertion, refinement, and extraction.[13] For direct knowledge insertion, the IF and THEN clauses of each instruction (rule) is translated into a pair of vectors A and B respectively. The vector pairs derived are then used as training patterns for inserting into a fusion ART network. During rule insertion, the vigilance parameters are set to 1s to ensure that each distinct rule is encoded by one category node.

For details on integrating domain knowledge into fusion ART, please refer to a recent paper.[14]

Fusion architecture for learning and cognition (FALCON)

Reinforcement learning is a paradigm wherein an autonomous system learns to adjust its behaviour based on reinforcement signals received from the environment. An instance of fusion ART, known as FALCON (fusion architecture for learning and cognition), learns mappings simultaneously across multi-modal input patterns, involving states, actions, and rewards, in an online and incremental manner. Compared with other ART-based reinforcement learning systems, FALCON presents a truly integrated solution in the sense that there is no implementation of a separate reinforcement learning module or Q-value table. Using competitive coding as the underlying principle of computation, the network dynamics encompasses several learning paradigms, including unsupervised learning, supervised learning, as well as reinforcement learning.

FALCON employs a three-channel architecture, comprising a category field ${\displaystyle F_{2}}$ and three pattern fields, namely a sensory field ${\displaystyle F_{1}^{c1}}$ for representing current states, a motor field ${\displaystyle F_{1}^{c2}}$ for representing actions, and a feedback field ${\displaystyle F_{1}^{c3}}$ for representing reward values. A class of FALCON networks, known as TD-FALCON,[8] incorporates Temporal Difference (TD) methods to estimate and learn value function Q(s,a), that indicates the goodness to take a certain action a in a given state s.

The general sense-act-learn algorithm for TD-FALCON is summarized. Given the current state s, the FALCON network is used to predict the value of performing each available action a in the action set A based on the corresponding state vector ${\displaystyle {\vec {s}}}$ and action vector ${\displaystyle {\vec {a}}}$. The value functions are then processed by an action selection strategy (also known as policy) to select an action. Upon receiving a feedback (if any) from the environment after performing the action, a TD formula is used to compute a new estimate of the Q-value for performing the chosen action in the current state. The new Q-value is then used as the teaching signal (represented as reward vector R) for FALCON to learn the association of the current state and the chosen action to the estimated value.

References

1. Y.R. Asfour, G.A. Carpenter, S. Grossberg, and G.W. Lesher. (1993) Fusion ARTMAP: an adaptive fuzzy network for multi-channel classification. In Proceedings of the Third International Conference on Industrial Fuzzy Control and Intelligent Systems (IFIS).
2. R.F. Harrison and J.M. Borges. (1995) Fusion ARTMAP: Clarification, Implementation and Developments. Research Report No. 589, Department of Automatic Control and Systems Engineering, The University of Sheffield.
3. Tan, A.-H., Carpenter, G. A. & Grossberg, S. (2007) Intelligence Through Interaction: Towards A Unified Theory for Learning . In proceedings, D. Liu et al. (Eds.): International Symposium on Neural Networks (ISNN'07), LNCS 4491, Part I, pp. 1098-1107.
4. Carpenter, G.A. & Grossberg, S. (2003), Adaptive Resonance Theory Archived 2006-05-19 at the Wayback Machine, In Michael A. Arbib (Ed.), The Handbook of Brain Theory and Neural Networks, Second Edition (pp. 87-90). Cambridge, MA: MIT Press
5. Wang, W.-W. & Tan, A.-H. (2016) Semantic Memory Modelling and Memory Interaction in Learning Agents. IEEE Transactions on Systems, Man and Cybernetics: Systems, in press.
6. Grossberg, S. (1987), Competitive learning: From interactive activation to adaptive resonance, Cognitive Science (Publication), 11, 23-63
7. Tan, A.-H. (1995). "Adaptive Resonance Associative Map" (PDF). Neural Networks. 8 (3): 437–446. doi:10.1016/0893-6080(94)00092-z.
8. Tan, A.-H., Lu, N.; Xiao, D (2008). "Integrating Temporal Difference Methods and Self-Organizing Neural Networks for Reinforcement Learning with Delayed Evaluative Feedback" (PDF). IEEE Transactions on Neural Networks. 9 (2): 230–244.CS1 maint: multiple names: authors list (link)
9. Tan, A.-H.; Soon, H.-S. (2000). Proceedings, Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD'00), LNAI. 1805: 173–176. Missing or empty |title= (help)
10. He, J.; Tan, A.-H.; Tan, C.-L. (2003). "On Machine Learning Methods for Chinese Document Classification" (PDF). Applied Intelligence. 18 (3): 311–322. doi:10.1023/A:1023202221875.
11. Tan, A.-H.; Ong, H.-L.; Pan, H.; Ng, J.; Li, Q.-X. (2004). "Towards Personalized Web Intelligence" (PDF). Knowledge and Information Systems. 6 (5): 595–616. doi:10.1007/s10115-003-0130-9.
12. Tan, A.-H.; Pan (2005). "Predictive Neural Networks for Gene Expression Data Analysis" (PDF). Neural Networks. 18 (3): 297–306. doi:10.1016/j.neunet.2005.01.003. PMID 15896577.
13. Tan, A.-H. (1997). "Cascade ARTMAP: Integrating Neural Computation and Symbolic Knowledge Processing" (PDF). IEEE Transactions on Neural Networks.
14. Teng, T.-H.; Tan, A.-H.; Zurada, J. (2015). "Self-Organizing Neural Networks Integrating Domain Knowledge and Reinforcement Learning" (PDF). IEEE Transactions on Neural Networks and Learning Systems. 26 (5): 889–902. doi:10.1109/tnnls.2014.2327636. PMID 25881365.