Free neutron decay

Outside the nucleus, free neutrons are unstable and have a mean lifetime of 880.2±1.0 s (about 14 minutes, 40 seconds).[1] Therefore, the half-life for this process (which differs from the mean lifetime by a factor of ln(2) ≈ 0.693) is 611±1 s (about 10 minutes, 11 seconds).[2] The beta decay of the neutron, described above, can be denoted as follows:[3]

n⁰
→
p⁺
+
e⁻
+
ν
_e

Feynman diagram for beta decay of the neutron

A schematic of the nucleus of an atom indicating
β⁻
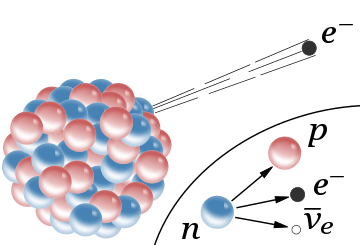
radiation, the emission of a fast electron from the nucleus (the accompanying antineutrino is omitted). In the Rutherford model for the nucleus, red spheres were protons with positive charge and blue spheres were protons tightly bound to an electron with no net charge.
The inset shows beta decay of a free neutron as it is understood today; an electron and antineutrino are created in this process.

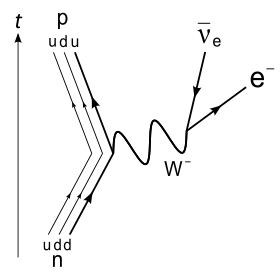
This decay, like any flavor-changing process, occurs through operation of the weak force. It involves the emission of a
W⁻
boson from one of the down quarks within the neutron, thereby converting the down quark into an up quark and the neutron into a proton; the
W⁻
then decays into the electron and the antineutrino. The following equations denote the same process as the first equation above, but also include the short-lived
W⁻
and describe the process on both the nucleon and the quark level:

n⁰
→
p⁺
+
W⁻
→
p⁺
+
e⁻
+
ν
_e

u

d

d
→
u

u

d
+
W⁻
→
u

u

d
+
e⁻
+
ν
_e

For the free neutron, the decay energy for this process (based on the rest masses of the neutron, proton and electron) is 0.782343 MeV. That is the difference between the rest mass of the neutron and the sum of the rest masses of the products. That difference has to be carried away as kinetic energy. The maximal energy of the beta decay electron (in the process wherein the neutrino receives a vanishingly small amount of kinetic energy) has been measured at 0.782 ± .013 MeV.[4] The latter number is not well-enough measured to determine the comparatively tiny rest mass of the neutrino (which must in theory be subtracted from the maximal electron kinetic energy); furthermore, neutrino mass is constrained by many other methods.

A small fraction (about one in 1000) of free neutrons decay with the same products, but add an extra particle in the form of an emitted gamma ray:

n⁰
→
p⁺
+
e⁻
+
ν
_e +
γ

This gamma ray may be thought of as a sort of "internal bremsstrahlung" that arises as the emitted beta particle (electron) interacts with the charge of the proton in an electromagnetic way. In this process, some of the decay energy is carried away as photon energy. Internal bremsstrahlung gamma ray production is also a minor feature of beta decays of bound neutrons, that is, those within a nucleus.

A very small minority of neutron decays (about four per million) are so-called "two-body (neutron) decays", in which a proton, electron and antineutrino are produced as usual, but the electron fails to gain the 13.6 eV necessary energy to escape the proton (the ionization energy of hydrogen), and therefore simply remains bound to it, as a neutral hydrogen atom (one of the "two bodies"). In this type of free neutron decay, in essence all of the neutron decay energy is carried off by the antineutrino (the other "body").

The transformation of a free proton to a neutron (plus a positron and a neutrino) is energetically impossible, since a free neutron has a greater mass than a free proton. However, see proton decay.

Neutron lifetime puzzle

While the neutron lifetime has been studied for decades, there currently exists a lack of consilience on its exact value, due to different results from two experimental methods ("bottle" versus "beam"[5]). While the error margin was once overlapping, increasing refinement in technique which should have resolved the issue has failed to demonstrate convergence to a single value.[6][7][8][9] The difference in mean lifetime values obtained as of 2014 was approximately 9 seconds.[7] Further, a prediction of the value based on quantum chromodynamics as of 2018 is still not sufficiently precise to support one over the other.[10] As discussed in [5], the beam test would be incorrect if there is a decay mode that does not produce a proton.

References

1. PDG 2018 value
2. J. Beringer et al. (Particle Data Group), Phys. Rev. D86, 010001 (2012) http://pdg.lbl.gov/2012/tables/rpp2012-sum-baryons.pdf
3. Particle Data Group Summary Data Table on Baryons. lbl.gov (2007). Retrieved on 2012-08-16.
4. Basic Ideas and Concepts in Nuclear Physics: An Introductory Approach, Third Edition K. Heyde Taylor & Francis 2004. Print ISBN 978-0-7503-0980-6. eBook ISBN 978-1-4200-5494-1. DOI: 10.1201/9781420054941.ch5 (full text).
5. Wolchover, Natalie (13 February 2018). "Neutron Lifetime Puzzle Deepens, but No Dark Matter Seen". Quanta Magazine. Retrieved 31 July 2018. When physicists strip neutrons from atomic nuclei, put them in a bottle, then count how many remain there after some time, they infer that neutrons radioactively decay in 14 minutes and 39 seconds, on average. But when other physicists generate beams of neutrons and tally the emerging protons — the particles that free neutrons decay into — they peg the average neutron lifetime at around 14 minutes and 48 seconds. The discrepancy between the “bottle” and “beam” measurements has persisted since both methods of gauging the neutron’s longevity began yielding results in the 1990s. At first, all the measurements were so imprecise that nobody worried. Gradually, though, both methods have improved, and still they disagree.
6. Paul, Stephan (2009). "The puzzle of neutron lifetime". Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 611 (2–3): 157–166. arXiv:0902.0169. Bibcode:2009NIMPA.611..157P. doi:10.1016/j.nima.2009.07.095. ISSN 0168-9002.
7. Moskowitz, Clara (2014). "Neutron death mystery has physicists stymied". Nature. doi:10.1038/nature.2014.15219. ISSN 1476-4687.
8. Greene, Geoffrey L.; Geltenbort, Peter (2016). "The Neutron Enigma". Scientific American. 314 (4): 36–41. Bibcode:2016SciAm.314d..36G. doi:10.1038/scientificamerican0416-36. ISSN 0036-8733. OSTI 1481712. PMID 27082189.
9. Mumm, Pieter (2018). "Resolving the neutron lifetime puzzle". Science. 360 (6389): 605–606. Bibcode:2018Sci...360..605M. doi:10.1126/science.aat7140. ISSN 0036-8075. PMID 29748273.
10. "Nuclear Scientists Calculate Value of Key Property that Drives Neutron Decay". Brookhaven National Laboratory. 30 May 2018. Retrieved 31 July 2018. The scientists have already used the new nucleon axial coupling calculation to derive a purely theoretical prediction of the lifetime of the neutron. Right now, this new value is consistent with the results from both types of experimental measurement, which differ by a mere 9 seconds. “We have a number for the neutron lifetime: 14 minutes and 40 seconds with an error bar of 14 seconds. That is right in the middle of the values measured by the two types of experiments, with an error bar that is big and overlaps both,” Rinaldi said.

Literature

• Б. Г. Ерозолимский (1975). "Бета-распад нейтрона". Успехи физических наук. 116 (1): 145–164.