Fredkin gate

The Fredkin gate (also CSWAP gate) is a computational circuit suitable for reversible computing, invented by Edward Fredkin. It is universal, which means that any logical or arithmetic operation can be constructed entirely of Fredkin gates. The Fredkin gate is a circuit or device with three inputs and three outputs that transmits the first bit unchanged and swaps the last two bits if, and only if, the first bit is 1.

Circuit representation of Fredkin gate

Definition

The basic Fredkin gate[1] is a controlled swap gate that maps three inputs (C, I₁, I₂) onto three outputs (C, O₁, O₂). The C input is mapped directly to the C output. If C = 0, no swap is performed; I₁ maps to O₁, and I₂ maps to O₂. Otherwise, the two outputs are swapped so that I₁ maps to O₂, and I₂ maps to O₁. It is easy to see that this circuit is reversible, i.e., "undoes" itself when run backwards. A generalized n×n Fredkin gate passes its first n-2 inputs unchanged to the corresponding outputs, and swaps its last two outputs if and only if the first n-2 inputs are all 1.

The Fredkin gate is the reversible three-bit gate that swaps the last two bits if, and only if, the first bit is 1.

Truth table

Permutation matrix form

INPUT			OUTPUT
C	I₁	I₂	C	O₁	O₂
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	0	1
1	1	1	1	1	1

${\begin{bmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\\end{bmatrix}}$

It has the useful property that the numbers of 0s and 1s are conserved throughout, which in the billiard ball model means the same number of balls are output as input. This corresponds nicely to the conservation of mass in physics, and helps to show that the model is not wasteful.

Truth functions with AND, OR, XOR, and NOT

The Fredkin gate can be defined using truth functions with AND, OR, XOR, and NOT, as follows:

O₁ = I₁ XOR S

O₂ = I₂ XOR S

C_out= C_in

where S = (I₁ XOR I₂) AND C

Alternatively:

O₁ = (NOT C AND I₁) OR (C AND I₂)

O₂ = (C AND I₁) OR (NOT C AND I₂)

C_out= C_in

Completeness

One way to see that the Fredkin gate is universal is to observe that it can be used to implement AND, NOT and OR:

If I₂ = 0, then O₂ = C AND I₁.

If I₂ = 1, then O₁ = C OR I₁.

If I₁ = 0 and I₂ = 1, then O₂ = NOT C.

Example

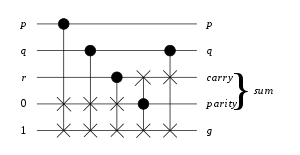
Three-bit full adder (add with carry) using five Fredkin gates

Three-bit full adder (add with carry) using five Fredkin gates. The "g" garbage output bit is (p NOR q) if r=0, and (p NAND q) if r=1.

Inputs on the left, including two constants, go through three gates to quickly determine the parity. The 0 and 1 bits swap places for each input bit that is set, resulting in parity bit on the 4th row and inverse of parity on 5th row.

Then the carry row and the inverse parity row swap if the parity bit is set and swap again if one of the p or q input bits are set (it doesn't matter which is used) and the resulting carry output appears on the 3rd row.

The p and q inputs are only used as gate controls so they appear unchanged in the output.

Quantum Fredkin gate

On March 25, 2016, researchers from Griffith University and the University of Queensland announced they had built a quantum Fredkin gate that uses the quantum entanglement of particles of light to swap qubits. The availability of quantum Fredkin gates may facilitate the construction of quantum computers.[2][3]

gollark: This is a false dichotomy.

gollark: But then I wouldn't have a computer. I need that.

gollark: Well, it's unsafe.

gollark: Really? I've seen a bunch of random Linux programs written in C.

gollark: I agree that writing everything in intensely horrific JS is bad. I just don't think that much application software which is currently written in C would become worse if written in something safer and higher level.

References

Brown, Julian, The Quest for the Quantum Computer, New York : Touchstone, 2000.
http://www.pcworld.com/article/3048763/hardware/quantum-computing-is-now-a-big-step-closer-thanks-to-this-new-breakthrough.html
A quantum Fredkin gate Raj B. Patel, Joseph Ho, Franck Ferreyrol, Timothy C. Ralph and Geoff J. Pryde, Science Advances, 25 Mar 2016, Vol. 2, no. 3, e1501531, DOI: 10.1126/sciadv.1501531