Folded cube graph
In graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.
| Folded cube graph | |
|---|---|
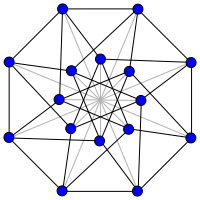 The order-5 folded cube graph (i.e, the Clebsch graph). | |
| Vertices | 2n−1 |
| Edges | 2n−2n |
| Diameter | floor(n/2) |
| Chromatic number | 2 (for even n), or 4 (when odd). |
| Properties | Regular graph Hamiltonian Distance-transitive. |
| Table of graphs and parameters | |
Construction
The folded cube graph of order k (containing 2k − 1 vertices) may be formed by adding edges between opposite pairs of vertices in a hypercube graph of order k − 1. (In a hypercube with 2n vertices, a pair of vertices are opposite if the shortest path between them has length n.) It can, equivalently, be formed from a hypercube graph (also) of order k, which has twice as many vertices, by identifying together (or contracting) every opposite pair of vertices.
Properties
An order-k folded cube graph is k-regular with 2k − 1 vertices and 2k − 2k edges.
The chromatic number of the order-k folded cube graph is two when k is even (that is, in this case, the graph is bipartite) and four when k is odd.[1] The odd girth of a folded cube of odd order is k, so for odd k greater than three the folded cube graphs provide a class of triangle-free graphs with chromatic number four and arbitrarily large odd girth. As a distance-regular graph with odd girth k and diameter (k − 1)/2, the folded cubes of odd order are examples of generalized odd graphs.[2]
When k is odd, the bipartite double cover of the order-k folded cube is the order-k cube from which it was formed. However, when k is even, the order-k cube is a double cover but not the bipartite double cover. In this case, the folded cube is itself already bipartite. Folded cube graphs inherit from their hypercube subgraphs the property of having a Hamiltonian cycle, and from the hypercubes that double cover them the property of being a distance-transitive graph.[3]
When k is odd, the order-k folded cube contains as a subgraph a complete binary tree with 2k − 1 nodes. However, when k is even, this is not possible, because in this case the folded cube is a bipartite graph with equal numbers of vertices on each side of the bipartition, very different from the nearly two-to-one ratio for the bipartition of a complete binary tree.[4]
Examples
- The folded cube graph of order three is a complete graph K4.
- The folded cube graph of order four is the complete bipartite graph K4,4.
- The folded cube graph of order five is the Clebsch graph.
- The folded cube graph of order six is the Kummer graph, i.e. the Levi graph of the Kummer point-plane configuration.
Applications
In parallel computing, folded cube graphs have been studied as a potential network topology, as an alternative to the hypercube. Compared to a hypercube, a folded cube with the same number of nodes has nearly the same vertex degree but only half the diameter. Efficient distributed algorithms (relative to those for a hypercube) are known for broadcasting information in a folded cube.[5]
See also
Notes
- Godsil (2004) provides a proof, and credits the result to Naserasr and Tardif.
- Van Dam & Haemers (2010).
- van Bon (2007).
- Choudam & Nandini (2004).
- El-Amawy & Latifi (1991); Varvarigos (1995).
References
- van Bon, John (2007), "Finite primitive distance-transitive graphs", European Journal of Combinatorics, 28 (2): 517–532, doi:10.1016/j.ejc.2005.04.014.
- Choudam, S. A.; Nandini, R. Usha (2004), "Complete binary trees in folded and enhanced cubes", Networks, 43 (4): 266–272, doi:10.1002/net.20002.
- Van Dam, Edwin; Haemers, Willem H. (2010), An Odd Characterization of the Generalized Odd Graphs, CentER Discussion Paper Series No. 2010-47, SSRN 1596575.
- El-Amawy, A.; Latifi, S. (1991), "Properties and performance of folded hypercubes", IEEE Trans. Parallel Distrib. Syst., 2 (1): 31–42, doi:10.1109/71.80187.
- Godsil, Chris (2004), Interesting graphs and their colourings, CiteSeerX 10.1.1.91.6390.
- Varvarigos, E. (1995), "Efficient routing algorithms for folded-cube networks", Proc. 14th Int. Phoenix Conf. on Computers and Communications, IEEE, pp. 143–151, doi:10.1109/PCCC.1995.472498.