Flory–Stockmayer theory

Flory–Stockmayer theory is a theory governing the cross-linking and gelation of step-growth polymers.[1] The Flory-Stockmayer theory represents an advancement from the Carothers equation, allowing for the identification of the gel point for polymer synthesis not at stoichiometric balance.[1] The theory was initially conceptualized by Paul Flory in 1941[1] and then was further developed by Walter Stockmayer in 1944 to include cross-linking with an arbitrary initial size distribution.[2] The Flory-Stockmayer theory was the first theory investigating percolation processes[3].

History

Gelation occurs when a polymer forms large interconnected polymer molecules through cross-linking.[1] In other words, polymer chains are cross-linked with other polymer chains to form an infinitely large molecule, interspersed with smaller complex molecules, shifting the polymer from a liquid to a network solid or gel phase. The Carothers equation is an effective method for calculating the degree of polymerization for stoichiometrically balanced reactions.[1] However, the Carothers equation is limited to branched systems, describing the degree of polymerization only at the onset of cross-linking. The Flory-Stockmayer Theory allows for the prediction of when gelation occurs using percent conversion of initial monomer and is not confined to cases of stoichiometric balance. Additionally, the Flory-Stockmayer Theory can be used to predict whether gelation is possible through analyzing the limiting reagent of the step-growth polymerization.[1]

Flory’s assumptions

In creating the Flory-Stockmayer Theory, Flory made three assumptions that affect the accuracy of this model.[1][4] These assumptions were

1. All functional groups on a branch unit are equally reactive
2. All reactions occur between A and B
3. There are no intramolecular reactions

As a result of these assumptions, a conversion slightly higher than that predicted by the Flory-Stockmayer Theory is commonly needed to actually create a polymer gel. Since steric hindrance effects prevent each functional group from being equally reactive and intramolecular reactions do occur, the gel forms at slightly higher conversion.[4]

General case

A general image of a multifunctional branch unit, ${\displaystyle A_{f}}$, reacting with bifunctional monomers with A and B functional groups to form a step-growth polymer.

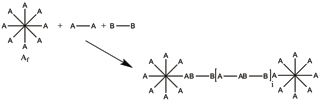
The Flory-Stockmayer Theory predicts the gel point for the system consisting of three types of monomer units[1][4][5][6]

linear units with two A-groups (concentration ${\displaystyle c_{1}}$),

linear units with two B groups (concentration ${\displaystyle c_{2}}$),

branched A units (concentration ${\displaystyle c_{3}}$).

The following definitions are used to formally define the system[1][4]

${\displaystyle f}$ is the number of reactive functional groups on the branch unit (i.e. the functionality of that branch unit)

${\displaystyle p_{A}}$ is the probability that A has reacted (conversion of A groups)

${\displaystyle p_{B}}$ is the probability that B has reacted (conversion of B groups)

${\displaystyle \rho ={\frac {fc_{3}}{2c_{1}+fc_{3}}}}$ is the ratio of number of A groups in the branch unit to the total number of A groups

${\displaystyle r={\frac {2c_{1}+fc_{3}}{2c_{2}}}={\frac {p_{B}}{p_{A}}}}$ is the ratio between total number of A and B groups. So that ${\displaystyle p_{B}=rp_{A}.}$

The theory states that the gelation occurs only if ${\displaystyle \alpha >\alpha _{c}}$, where

${\displaystyle \alpha _{c}={\frac {1}{f-1}}}$

is the critical value for cross-linking and ${\displaystyle \alpha }$ is presented as a function of ${\displaystyle p_{A}}$,

${\displaystyle \alpha (p_{A})={\frac {rp_{A}^{2}\rho }{1-rp_{A}^{2}(1-\rho )}}}$

or, alternatively, as a function of ${\displaystyle p_{B}}$,

${\displaystyle \alpha (p_{B})={\frac {p_{B}^{2}\rho }{r-p_{B}^{2}(1-\rho )}}}$.

One may now substitute expressions for ${\displaystyle r,\rho }$ into definition of ${\displaystyle \alpha }$ and obtain the critical values of ${\displaystyle p_{A},(p_{B})}$ that admit gelation. Thus gelation occurs if

${\displaystyle p_{A}>{\sqrt {\frac {\alpha _{c}}{r(\alpha _{c}+\rho -\alpha _{c}\rho )}}}.}$

alternatively, the same condition for ${\displaystyle p_{B}}$ reads,

${\displaystyle p_{B}>{\sqrt {\frac {r\alpha _{c}}{\alpha _{c}+\rho -\alpha _{c}\rho }}}}$

The both inequalities are equivalent and one may use the one that is more convenient. For instance, depending on which conversion ${\displaystyle p_{A}}$ or ${\displaystyle p_{B}}$ is resolved analytically.

Trifunctional A monomer with difunctional B monomer

A trifunctional branch unit with A functional group reacting with a bifunctional branch unit with a B functional group, forming a continuous step-growth polymer molecule.

${\displaystyle \alpha _{c}={\frac {1}{f-1}}={\frac {1}{3-1}}={\frac {1}{2}}}$

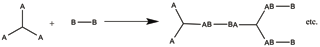
Since all the A functional groups are from the trifunctional monomer, ρ = 1 and

${\displaystyle \alpha ={\frac {\frac {p_{B}^{2}\rho }{r}}{1-{\frac {p_{B}^{2}}{r(1-\rho )}}}}={\frac {p_{B}^{2}}{r}}}$

Therefore, gelation occurs when

${\displaystyle {\frac {p_{B}^{2}}{r}}>\alpha _{c}}$

or when,

${\displaystyle p_{B}>{\sqrt {\frac {r}{2}}}}$

Similarly, gelation occurs when

${\displaystyle p_{A}>{\sqrt {\frac {1}{2r}}}}$

References

1. Flory, P.J. (1941). "Molecular Size Distribution in Three Dimensional Polymers I. Gelation". J. Am. Chem. Soc. 63, 3083
2. Stockmayer, Walter H.(1944). "Theory of Molecular Size Distribution and Gel Formation in Branched Polymers II. General Cross Linking". Journal of Chemical Physics. 12,4, 125
3. Sahini, M.; Sahimi, M. (2003-07-13). Applications Of Percolation Theory. CRC Press. ISBN 978-0-203-22153-2.
4. Stauffer, Dietrich, et al.(1982) "Gelation and Critical Phenomena". Advances in Polymer Science 44, 103
5. Flory, P.J.(1941). "Molecular Size Distribution in Three Dimensional Polymers II. Trifunctional Branching Units". J. Am. Chem. Soc. 63, 3091
6. Flory, P.J. (1941). "Molecular Size Distribution in Three Dimensional Polymers III. Tetrafunctional Branching Units". J. Am. Chem. Soc. 63, 3096