Fixed end moment

The fixed end moments are reaction moments developed in a beam member under certain load conditions with both ends fixed. A beam with both ends fixed is statically indeterminate to the 2nd degree, and any structural analysis method applicable on statically indeterminate beams can be used to calculate the fixed end moments.

Examples

In the following examples, clockwise moments are positive.

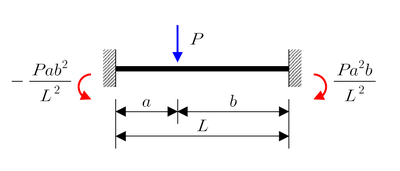Concentrated load of magnitude P	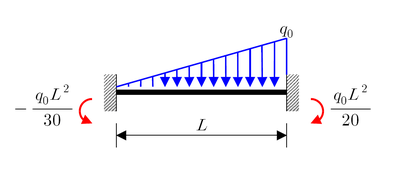Linearly distributed load of maximum intensity q0
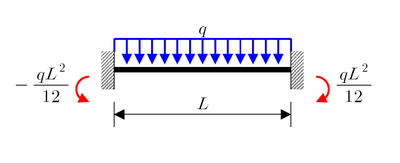Uniformly distributed load of intensity q	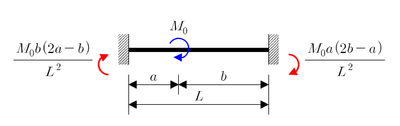Couple of magnitude M0

The two cases with distributed loads can be derived from the case with concentrated load by integration. For example, when a uniformly distributed load of intensity ${\displaystyle q}$ is acting on a beam, then an infinitely small part ${\displaystyle dx}$ distance ${\displaystyle x}$ apart from the left end of this beam can be seen as being under a concentrated load of magnitude ${\displaystyle qdx}$. Then,

${\displaystyle M_{\mathrm {right} }^{\mathrm {fixed} }=\int _{0}^{L}{\frac {qdx\,x^{2}(L-x)}{L^{2}}}={\frac {qL^{2}}{12}}}$

${\displaystyle M_{\mathrm {left} }^{\mathrm {fixed} }=\int _{0}^{L}\left\{-{\frac {qdx\,x^{2}(L-x)}{L^{2}}}\right\}=-{\frac {qL^{2}}{12}}}$

Where the expressions within the integrals on the right hand sides are the fixed end moments caused by the concentrated load ${\displaystyle qdx}$.

For the case with linearly distributed load of maximum intensity ${\displaystyle q_{0}}$,

${\displaystyle M_{\mathrm {right} }^{\mathrm {fixed} }=\int _{0}^{L}q_{0}{\frac {x}{L}}dx{\frac {x^{2}(L-x)}{L^{2}}}={\frac {q_{0}L^{2}}{20}}}$

${\displaystyle M_{\mathrm {left} }^{\mathrm {fixed} }=\int _{0}^{L}\left\{-q_{0}{\frac {x}{L}}dx{\frac {x(L-x)^{2}}{L^{2}}}\right\}=-{\frac {q_{0}L^{2}}{30}}}$

See also

• Moment distribution method
• Statically Indeterminate
• Slope deflection method
• Matrix method

References

• Yang, Chang-hyeon (2001-01-10). Structural Analysis (in Korean) (4th ed.). Seoul: Cheong Moon Gak Publishers. ISBN 89-7088-709-1. Archived from the original on 2007-10-08. Retrieved 2007-09-03.