Finsler–Hadwiger theorem

The Finsler–Hadwiger theorem is statement in Euclidean plane geometry that describes a third square derived from any two squares that share a vertex. The theorem is named after Paul Finsler and Hugo Hadwiger, who published it in 1937 as part of the same paper in which they published the Hadwiger–Finsler inequality relating the side lengths and area of a triangle.[1]

This article is about the theorem on squares. For the inequality on the sides and area of a triangle, see Hadwiger–Finsler inequality.
Finsler-Hadwiger theorem

Statement

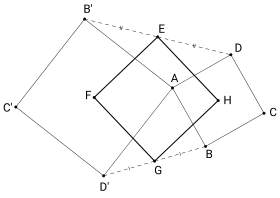
To state the theorem, suppose that ABCD and AB'C'D' are two squares with common vertex A. Let E and G be the midpoints of B'D and D'B respectively, and let F and H be the centers of the two squares. Then the theorem states that the quadrilateral EFGH is a square as well.[2]

The square EFGH is called the Finsler–Hadwiger square of the two given squares.[3]

Application

Repeated application of the Finsler–Hadwiger theorem can be used to prove Van Aubel's theorem, on the congruence and perpendicularity of segments through centers of four squares constructed on the sides of an arbitrary quadrilateral. Each pair of consecutive squares forms an instance of the theorem, and the two pairs of opposite Finsler–Hadwiger squares of those instances form another two instances of the theorem, having the same derived square.[4]

gollark: The best (for power output) reaction is D-T, it seems.
gollark: (note: may not actually cancel out)
gollark: You can make the bath contain plasma *and* neutron fluid *and* liquid helium, so it cancels out.
gollark: Idea: fusion plasma bathing experience.
gollark: I just run all my reactors so that they need no manual intervention at all.

References
  1. Finsler, Paul; Hadwiger, Hugo (1937), "Einige Relationen im Dreieck", Commentarii Mathematici Helvetici (in German), 10 (1): 316–326, doi:10.1007/BF01214300, MR 1509584. See in particular p. 324.
  2. Alsina, Claudi; Nelsen, Roger B. (2010), "The Finsler–Hadwiger Theorem 8.5", Charming Proofs: A Journey Into Elegant Mathematics, Mathematical Association of America, p. 125, ISBN 9780883853481.
  3. Detemple, Duane; Harold, Sonia (1996), "A round-up of square problems", Mathematics Magazine, 69 (1): 15–27, doi:10.1080/0025570X.1996.11996375, JSTOR 2691390, MR 1573131. See problem 8, pp. 20–21.
  4. Detemple & Harold (1996), problem 15, pp. 25–26.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.