Fenchel's duality theorem

In mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel.

Let ƒ be a proper convex function on Rⁿ and let g be a proper concave function on Rⁿ. Then, if regularity conditions are satisfied,

${\displaystyle \inf _{x}(f(x)-g(x))=\sup _{p}(g_{\star }(p)-f^{\star }(p)).}$

where ƒ ^* is the convex conjugate of ƒ (also referred to as the Fenchel–Legendre transform) and g _* is the concave conjugate of g. That is,

${\displaystyle f^{\star }\left(x^{*}\right):=\sup \left\{\left.\left\langle x^{*},x\right\rangle -f\left(x\right)\right|x\in \mathbb {R} ^{n}\right\}}$

${\displaystyle g_{\star }\left(x^{*}\right):=\inf \left\{\left.\left\langle x^{*},x\right\rangle -g\left(x\right)\right|x\in \mathbb {R} ^{n}\right\}}$

Mathematical theorem

Let X and Y be Banach spaces, ${\displaystyle f:X\to \mathbb {R} \cup \{+\infty \}}$ and ${\displaystyle g:Y\to \mathbb {R} \cup \{+\infty \}}$ be convex functions and ${\displaystyle A:X\to Y}$ be a bounded linear map. Then the Fenchel problems:

${\displaystyle p^{*}=\inf _{x\in X}\{f(x)+g(Ax)\}}$

${\displaystyle d^{*}=\sup _{y^{*}\in Y^{*}}\{-f^{*}(A^{*}y^{*})-g^{*}(-y^{*})\}}$

satisfy weak duality, i.e. ${\displaystyle p^{*}\geq d^{*}}$. Note that ${\displaystyle f^{*},g^{*}}$ are the convex conjugates of f,g respectively, and ${\displaystyle A^{*}}$ is the adjoint operator. The perturbation function for this dual problem is given by ${\displaystyle F(x,y)=f(x)+g(Ax-y)}$.

Suppose that f,g, and A satisfy either

1. f and g are lower semi-continuous and ${\displaystyle 0\in \operatorname {core} (\operatorname {dom} g-A\operatorname {dom} f)}$ where ${\displaystyle \operatorname {core} }$ is the algebraic interior and ${\displaystyle \operatorname {dom} h}$, where h is some function, is the set ${\displaystyle \{z:h(z)<+\infty \}}$, or
2. ${\displaystyle A\operatorname {dom} f\cap \operatorname {cont} g\neq \emptyset }$ where ${\displaystyle \operatorname {cont} }$ are the points where the function is continuous.

Then strong duality holds, i.e. ${\displaystyle p^{*}=d^{*}}$. If ${\displaystyle d^{*}\in \mathbb {R} }$ then supremum is attained.[1]

One-dimensional illustration

In the following figure, the minimization problem on the left side of the equation is illustrated. One seeks to vary x such that the vertical distance between the convex and concave curves at x is as small as possible. The position of the vertical line in the figure is the (approximate) optimum.

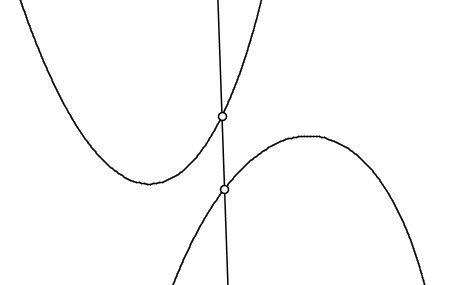
The next figure illustrates the maximization problem on the right hand side of the above equation. Tangents are drawn to each of the two curves such that both tangents have the same slope p. The problem is to adjust p in such a way that the two tangents are as far away from each other as possible (more precisely, such that the points where they intersect the y-axis are as far from each other as possible). Imagine the two tangents as metal bars with vertical springs between them that push them apart and against the two parabolas that are fixed in place.

Fenchel's theorem states that the two problems have the same solution. The points having the minimum vertical separation are also the tangency points for the maximally separated parallel tangents.

See also

• Legendre transformation
• Convex conjugate
• Moreau's theorem
• Wolfe duality
• Werner Fenchel

References

1. Borwein, Jonathan; Zhu, Qiji (2005). Techniques of Variational Analysis. Springer. pp. 135–137. ISBN 978-1-4419-2026-3.

• Bauschke, Heinz H.; Combettes, Patrick L. (2017). "Fenchel–Rockafellar Duality". Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer. pp. 247–262. doi:10.1007/978-3-319-48311-5_15. ISBN 978-3-319-48310-8.
• Rockafellar, Ralph Tyrrell (1996). Convex Analysis. Princeton University Press. p. 327. ISBN 0-691-01586-4.