Fejér kernel

In mathematics, the Fejér kernel is a summability kernel used to express the effect of Cesàro summation on Fourier series. It is a non-negative kernel, giving rise to an approximate identity. It is named after the Hungarian mathematician Lipót Fejér (1880–1959).

Plot of several Fejér kernels

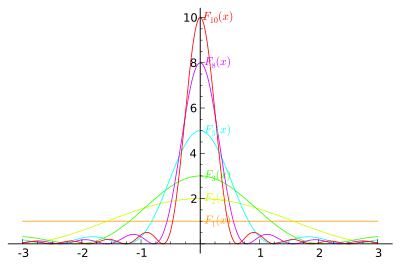
Definition

The Fejér kernel is defined as

${\displaystyle F_{n}(x)={\frac {1}{n}}\sum _{k=0}^{n-1}D_{k}(x),}$

where

${\displaystyle D_{k}(x)=\sum _{s=-k}^{k}{\rm {e}}^{isx}}$

is the kth order Dirichlet kernel. It can also be written in a closed form as

${\displaystyle F_{n}(x)={\frac {1}{n}}\left({\frac {\sin {\frac {nx}{2}}}{\sin {\frac {x}{2}}}}\right)^{2}={\frac {1}{n}}\left({\frac {1-\cos(nx)}{1-\cos x}}\right)}$,

where this expression is defined.[1]

The Fejér kernel can also be expressed as

${\displaystyle F_{n}(x)=\sum _{|j|\leq n-1}\left(1-{\frac {|j|}{n}}\right)e^{ijx}}$.

Properties

The Fejér kernel is a positive summability kernel. An important property of the Fejér kernel is ${\displaystyle F_{n}(x)\geq 0}$ with average value of ${\displaystyle 1}$.

Convolution

The convolution F_n is positive: for ${\displaystyle f\geq 0}$ of period ${\displaystyle 2\pi }$ it satisfies

${\displaystyle 0\leq (f*F_{n})(x)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(y)F_{n}(x-y)\,dy.}$

Since ${\displaystyle f*D_{n}=S_{n}(f)=\sum _{|j|\leq n}{\widehat {f}}_{j}e^{ijx}}$, we have ${\displaystyle f*F_{n}={\frac {1}{n}}\sum _{k=0}^{n-1}S_{k}(f)}$, which is Cesàro summation of Fourier series.

By Young's convolution inequality,

${\displaystyle \|F_{n}*f\|_{L^{p}([-\pi ,\pi ])}\leq \|f\|_{L^{p}([-\pi ,\pi ])}}$ for every ${\displaystyle 1\leq p\leq \infty }$

for ${\displaystyle f\in L^{p}}$.

Additionally, if ${\displaystyle f\in L^{1}([-\pi ,\pi ])}$, then

${\displaystyle f*F_{n}\rightarrow f}$ a.e.

Since ${\displaystyle [-\pi ,\pi ]}$ is finite, ${\displaystyle L^{1}([-\pi ,\pi ])\supset L^{2}([-\pi ,\pi ])\supset \cdots \supset L^{\infty }([-\pi ,\pi ])}$, so the result holds for other ${\displaystyle L^{p}}$ spaces, ${\displaystyle p\geq 1}$ as well.

If ${\displaystyle f}$ is continuous, then the convergence is uniform, yielding a proof of the Weierstrass theorem.

• One consequence of the pointwise a.e. convergence is the uniqueness of Fourier coefficients: If ${\displaystyle f,g\in L^{1}}$ with ${\displaystyle {\hat {f}}={\hat {g}}}$, then ${\displaystyle f=g}$ a.e. This follows from writing ${\displaystyle f*F_{n}=\sum _{|j|\leq n}\left(1-{\frac {|j|}{n}}\right){\hat {f}}_{j}e^{ijt}}$, which depends only on the Fourier coefficients.
• A second consequence is that if ${\displaystyle \lim _{n\to \infty }S_{n}(f)}$ exists a.e., then ${\displaystyle \lim _{n\to \infty }F_{n}(f)=f}$ a.e., since Cesàro means ${\displaystyle F_{n}*f}$ converge to the original sequence limit if it exists.

See also

• Fejér's theorem
• Dirichlet kernel
• Gibbs phenomenon
• Charles Jean de la Vallée-Poussin

References

1. Hoffman, Kenneth (1988). Banach Spaces of Analytic Functions. Dover. p. 17. ISBN 0-486-45874-1.