Euclidean random matrix
An N×N Euclidean random matrix  is defined with the help of an arbitrary deterministic function f(r, r′) and of N points {ri} randomly distributed in a region V of d-dimensional Euclidean space. The element Aij of the matrix is equal to f(ri, rj): Aij = f(ri, rj).
History
Euclidean random matrices were first introduced in 1999.[1] They studied a special case of functions f that depend only on the distances between the pairs of points: f(r, r′) = f(r - r′) and imposed an additional condition on the diagonal elements Aii,
- Aij = f(ri - rj) - u δij∑kf(ri - rk),
motivated by the physical context in which they studied the matrix. A Euclidean distance matrix is a particular example of Euclidean random matrix with either f(ri - rj) = |ri - rj|2 or f(ri - rj) = |ri - rj|.[2]
For example, in many biological networks, the strength of interaction between two nodes depends on the physical proximity of those nodes. Spatial interactions between nodes can be modelled as a Euclidean random matrix, if nodes are placed randomly in space.[3][4]
Properties
Because the positions of the points {ri} are random, the matrix elements Aij are random too. Moreover, because the N×N elements are completely determined by only N points and, typically, one is interested in N≫d, strong correlations exist between different elements.
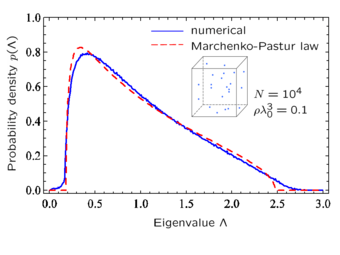
Hermitian Euclidean random matrices
Hermitian Euclidean random matrices appear in various physical contexts, including supercooled liquids,[5] phonons in disordered systems,[6] and waves in random media.[7]
Example 1: Consider the matrix  generated by the function f(r, r′) = sin(k0|r-r′|)/(k0|r-r′|), with k0 = 2π/λ0. This matrix is Hermitian and its eigenvalues Λ are real. For N points distributed randomly in a cube of side L and volume V = L3, one can show[7] that the probability distribution of Λ is approximately given by the Marchenko-Pastur law, if the density of points ρ = N/V obeys ρλ03 ≤ 1 and 2.8N/(k0 L)2 < 1 (see figure).
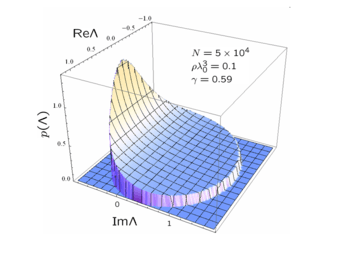
Non-Hermitian Euclidean random matrices
A theory for the eigenvalue density of large (N≫1) non-Hermitian Euclidean random matrices has been developed[8] and has been applied to study the problem of random laser.[9]
Example 2: Consider the matrix  generated by the function f(r, r′) = exp(ik0|r-r′|)/(k0|r-r′|), with k0 = 2π/λ0 and f(r= r′) = 0. This matrix is not Hermitian and its eigenvalues Λ are complex. The probability distribution of Λ can be found analytically[8] if the density of point ρ = N/V obeys ρλ03 ≤ 1 and 9N/(8k0 R)2 < 1 (see figure).
References
- Mezard, M.; Parisi, G.; Zee, A. (1999). "Spectra of euclidean random matrices". Nuclear Physics B. 559 (3): 689–701. arXiv:cond-mat/9906135. Bibcode:1999NuPhB.559..689M. doi:10.1016/S0550-3213(99)00428-9.
- Bogomolny, E.; Bohigas, O.; Schmit, C. (2003). "Spectral properties of distance matrices". Journal of Physics A: Mathematical and General. 36 (12): 3595–3616. arXiv:nlin/0301044. Bibcode:2003JPhA...36.3595B. doi:10.1088/0305-4470/36/12/341.
- Muir, Dylan; Mrsic-Flogel, Thomas (2015). "Eigenspectrum bounds for semirandom matrices with modular and spatial structure for neural networks". Phys. Rev. E. 91: 042808. Bibcode:2015PhRvE..91d2808M. doi:10.1103/PhysRevE.91.042808.
- Grilli, Jacopo; Barabás, György; Allesina, Stefano (2015). "Metapopulation Persistence in Random Fragmented Landscapes". PLOS Computational Biology. 11 (5): e1004251. Bibcode:2015PLSCB..11E4251G. doi:10.1371/journal.pcbi.1004251. ISSN 1553-7358. PMC 4439033.
- Grigera, T. S.; Martín-Mayor, V.; Parisi, G.; Verrocchio, P. (2003). "Phonon interpretation of the 'boson peak' in supercooled liquids". Nature. 422 (6929): 289–292. Bibcode:2003Natur.422..289G. doi:10.1038/nature01475. PMID 12646916.
- Amir, A.; Oreg, Y.; Imry, Y. (2010). "Localization, Anomalous Diffusion, and Slow Relaxations: A Random Distance Matrix Approach". Physical Review Letters. 105 (7): 070601. arXiv:1002.2123. Bibcode:2010PhRvL.105g0601A. doi:10.1103/PhysRevLett.105.070601. PMID 20868026.
- Skipetrov, S. E.; Goetschy, A. (2011). "Eigenvalue distributions of large Euclidean random matrices for waves in random media". Journal of Physics A: Mathematical and Theoretical. 44 (6): 065102. arXiv:1007.1379. Bibcode:2011JPhA...44f5102S. doi:10.1088/1751-8113/44/6/065102.
- Goetschy, A.; Skipetrov, S. (2011). "Non-Hermitian Euclidean random matrix theory". Physical Review E. 84. arXiv:1102.1850. Bibcode:2011PhRvE..84a1150G. doi:10.1103/PhysRevE.84.011150.
- Goetschy, A.; Skipetrov, S. E. (2011). "Euclidean matrix theory of random lasing in a cloud of cold atoms". EPL. 96 (3): 34005. arXiv:1104.2711. Bibcode:2011EL.....9634005G. doi:10.1209/0295-5075/96/34005.