Equation xʸ = yˣ

In general, exponentiation fails to be commutative. However, the equation ${\displaystyle x^{y}=y^{x}}$ holds in special cases, such as ${\displaystyle x=2,\ y=4.}$[1]

Graph of x^y = y^x.

History

The equation ${\displaystyle x^{y}=y^{x}}$ is mentioned in a letter of Bernoulli to Goldbach (29 June 1728[2]). The letter contains a statement that when ${\displaystyle x\neq y,}$ the only solutions in natural numbers are ${\displaystyle (2,4)}$ and ${\displaystyle (4,2),}$ although there are infinitely many solutions in rational numbers.[3][4] The reply by Goldbach (31 January 1729[2]) contains general solution of the equation, obtained by substituting ${\displaystyle y=vx.}$[3] A similar solution was found by Euler.[4]

J. van Hengel pointed out that if ${\displaystyle r,n}$ are positive integers with ${\displaystyle r\geq 3}$, then ${\displaystyle r^{r+n}>(r+n)^{r};}$ therefore it is enough to consider possibilities ${\displaystyle x=1}$ and ${\displaystyle x=2}$ in order to find solutions in natural numbers.[4][5]

The problem was discussed in a number of publications.[2][3][4] In 1960, the equation was among the questions on the William Lowell Putnam Competition,[6][7] which prompted Alvin Hausner to extend results to algebraic number fields.[3][8]

Positive real solutions

Main source:[1]

An infinite set of trivial solutions in positive real numbers is given by ${\displaystyle x=y.}$

Nontrivial solutions can be found by assuming ${\displaystyle x\neq y}$ and letting ${\displaystyle y=vx.}$ Then

${\displaystyle (vx)^{x}=x^{vx}=(x^{v})^{x}.}$

Raising both sides to the power ${\displaystyle {\tfrac {1}{x}}}$ and dividing by ${\displaystyle x}$, we get

${\displaystyle v=x^{v-1}.}$

Then nontrivial solutions in positive real numbers are expressed as

${\displaystyle x=v^{1/(v-1)},}$

${\displaystyle y=v^{v/(v-1)}.}$

Setting ${\displaystyle v=2}$ or ${\displaystyle v={\tfrac {1}{2}}}$ generates the nontrivial solution in positive integers, ${\displaystyle 4^{2}=2^{4}.}$

Other pairs consisting of algebraic numbers exist, such as ${\displaystyle {\sqrt {3}}}$ and ${\displaystyle 3{\sqrt {3}}}$, as well as ${\displaystyle {\sqrt[{3}]{4}}}$ and ${\displaystyle 4{\sqrt[{3}]{4}}}$.

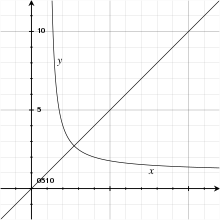
The trivial and non-trivial solutions intersect when ${\displaystyle v=1}$. The equations above cannot be evaluated directly, but we can take the limit as ${\displaystyle v\to 1}$. This is most conveniently done by substituting ${\displaystyle v=1+1/n}$ and letting ${\displaystyle n\to \infty }$, so

${\displaystyle x=\lim _{v\to 1}v^{1/(v-1)}=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e.}$

Thus, the line ${\displaystyle y=x}$ and the curve for ${\displaystyle x^{y}-y^{x}=0,\,\,y\neq x}$ intersect at x = y = e.

As ${\displaystyle x\to \infty }$, the nontrivial solution asymptotes to the line ${\displaystyle y=1}$. A more complete asymptotic form is

${\displaystyle y=1+{\frac {\ln x}{x}}+{\frac {3}{2}}{\frac {(\ln x)^{2}}{x^{2}}}+\cdots .}$

Similar graphs

The equation ${\displaystyle {\sqrt[{x}]{y}}={\sqrt[{y}]{x}}}$ produces a graph where the line and curve intersect at ${\displaystyle 1/e}$. The curve also terminates at (0, 1) and (1, 0), instead of continuing on to infinity.

The equation ${\displaystyle \log _{x}(y)=\log _{y}(x)}$ produces a graph where the curve and line intersect at (1, 1). The curve becomes asymptotic to 0, as opposed to 1; it is, in fact, the positive section of y = 1/x. The equations of the curves in the other two equations is unknown.

References

1. Lóczi, Lajos. "On commutative and associative powers". KöMaL. Archived from the original on 2002-10-15. Translation of: "Mikor kommutatív, illetve asszociatív a hatványozás?" (in Hungarian). Archived from the original on 2016-05-06.
2. Singmaster, David. "Sources in recreational mathematics: an annotated bibliography. 8th preliminary edition". Archived from the original on April 16, 2004.CS1 maint: unfit url (link)
3. Sved, Marta (1990). "On the Rational Solutions of x^y = y^x" (PDF). Mathematics Magazine. Archived from the original (PDF) on 2016-03-04.
4. Dickson, Leonard Eugene (1920), "Rational solutions of x^y = y^x", History of the Theory of Numbers, II, Washington, p. 687
5. van Hengel, Johann (1888). "Beweis des Satzes, dass unter allen reellen positiven ganzen Zahlen nur das Zahlenpaar 4 und 2 für a und b der Gleichung a^b = b^a genügt". Cite journal requires |journal= (help)
6. Gleason, A. M.; Greenwood, R. E.; Kelly, L. M. (1980), "The twenty-first William Lowell Putnam mathematical competition (December 3, 1960), afternoon session, problem 1", The William Lowell Putnam mathematical competition problems and solutions: 1938-1964, MAA, p. 59, ISBN 0-88385-428-7
7. "21st Putnam 1960. Problem B1". 20 Oct 1999. Archived from the original on 2008-03-30.CS1 maint: BOT: original-url status unknown (link)
8. Hausner, Alvin (November 1961). "Algebraic Number Fields and the Diophantine Equation mⁿ = n^m". The American Mathematical Monthly. 68 (9): 856–861. doi:10.1080/00029890.1961.11989781. ISSN 0002-9890.

External links

• "Rational Solutions to x^y = y^x". CTK Wiki Math.
• "x^y = y^x - commuting powers". Arithmetical and Analytical Puzzles. Torsten Sillke. Archived from the original on 2015-12-28.
• dborkovitz (2012-01-29). "Parametric Graph of x^y=y^x". GeoGebra.
• OEIS sequence A073084 (Decimal expansion of -x, where x is the negative solution to the equation 2^x = x^2)