Encompassment ordering
In theoretical computer science, in particular in automated theorem proving and term rewriting, the containment,[1] or encompassment, preorder (≤) on the set of terms, is defined by[2]
- s ≤ t if a subterm of t is a substitution instance of s.
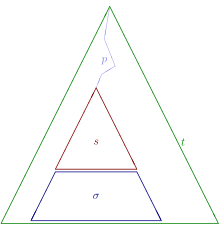
Triangle diagram of two terms s ≤ t related by the encompassment preorder.
It is used e.g. in the Knuth–Bendix completion algorithm.
Properties
- Encompassment is a preorder, i.e. reflexive and transitive, but not anti-symmetric,[note 1] nor total[note 2]
- The corresponding equivalence relation, defined by s ~ t if s ≤ t ≤ s, is equality modulo renaming.
- s ≤ t whenever s is a subterm of t.
- s ≤ t whenever t is a substitution instance of s.
- The union of any well-founded rewrite order R[note 3] with (<) is well-founded, where (<) denotes the irreflexive kernel of (≤).[3] In particular, (<) itself is well-founded.
Notes
- since both f(x) ≤ f(y) and f(y) ≤ f(x) for variable symbols x, y and a function symbol f
- since neither a ≤ b nor b ≤ a for distinct constant symbols a, b
- i.e. irreflexive, transitive, and well-founded binary relation R such that sRt implies u[sσ]p R u[tσ]p for all terms s, t, u, each path p of u, and each substitution σ
gollark: Oh, not that... it should run over discord channels though.
gollark: Channel based... Discord channels?
gollark: (Was on clipboard)
gollark: Your thing allocates a new string for every single Your thing allocates a new string for every single Your thing allocates a new string for every single Your thing allocates a new string for every single Your thing allocates a new string for every single Your thing allocates a new string for every single
gollark: Yes.
References
- Gerard Huet (1981). "A Complete Proof of Correctness of the Knuth–Bendix Completion Algorithm". J. Comput. Syst. Sci. 23 (1): 11–21. doi:10.1016/0022-0000(81)90002-7.
- N. Dershowitz, J.-P. Jouannaud (1990). Jan van Leeuwen (ed.). Rewrite Systems. Handbook of Theoretical Computer Science. B. Elsevier. pp. 243–320. Here:sect.2.1, p. 250
- Dershowitz, Jouannaud (1990), sect.5.4, p. 278; somewhat sloppy, R is required to be a "terminating rewrite relation" there.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.