Eötvös experiment

The Eötvös experiment was a famous physics experiment that measured the correlation between inertial mass and gravitational mass, demonstrating that the two were one and the same, something that had long been suspected but never demonstrated with the same accuracy. The earliest experiments were done by Isaac Newton (1642–1727) and improved upon by Friedrich Wilhelm Bessel (1784–1846).[1] A much more accurate experiment using a torsion balance was carried out by Loránd Eötvös starting around 1885, with further improvements in a lengthy run between 1906 and 1909. Eötvös's team followed this with a series of similar but more accurate experiments, as well as experiments with different types of materials and in different locations around the Earth, all of which demonstrated the same equivalence in mass. In turn, these experiments led to the modern understanding of the equivalence principle encoded in general relativity, which states that the gravitational and inertial masses are the same.

See also: Equivalence principle

It is sufficient for the inertial mass to be proportional to the gravitational mass. Any multiplicative constant will be absorbed in the definition of the unit of force.[2]

Eötvös's original experiment
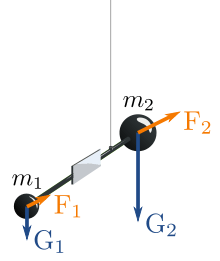
If the ratio of F1 to F2 differed from the ratio of G1 to G2, the rod would rotate. The mirror is used to monitor the rotation.
Direction of the centrifugal force in relation to gravity on the surface of earth.

Eötvös's original experimental device consisted of two masses on opposite ends of a rod, hung from a thin fiber. A mirror attached to the rod, or fiber, reflected light into a small telescope. Even tiny changes in the rotation of the rod would cause the light beam to be deflected, which would in turn cause a noticeable change when magnified by the telescope.

As seen from the Earth's frame of reference (or "lab frame", which is not an inertial frame of reference), the primary forces acting on the balanced masses are the string tension, gravity, and the centrifugal force due to the rotation of the Earth. Gravity is calculated by Newton's law of universal gravitation, which depends on gravitational mass. The centrifugal force is calculated by Newton's laws of motion and depends on inertial mass.

The experiment was arranged so that if the two types of masses were different, the two forces will not act in exactly the same way on the two bodies, and over time the rod will rotate. As seen from the rotating "lab frame", the string tension plus the (much smaller) centrifugal force cancels the weight (as vectors), while as seen from any inertial frame the (vector) sum of the weight and the tension makes the object rotate along with the earth.

For the rod to be at rest in the lab frame, the reactions, on the rod, of the tensions acting on each body, must create a zero net torque (the only degree of freedom is rotation on the horizontal plane). Supposing that the system was constantly at rest – this meaning mechanical equilibrium (i.e. net forces and torques zero) – with the two bodies thus hanging also at rest, but having different centrifugal forces upon them and consequently exerting different torques on the rod through the reactions of the tensions, the rod then would spontaneously rotate, in contradiction with our assumption that the system is at rest. So the system cannot exist in this state; any difference between the centrifugal forces on the two bodies will set the rod in rotation.

Further improvements

Initial experiments around 1885 demonstrated that there was no apparent difference, and Eötvös improved the experiment to demonstrate this with more accuracy. In 1889 he used the device with different types of sample materials to see if there was any change in gravitational force due to materials. This experiment proved that no such change could be measured, to a claimed accuracy of 1 in 20 million. In 1890 he published these results, as well as a measurement of the mass of Gellért Hill in Budapest.[3]

The next year he started work on a modified version of the device, which he called the "horizontal variometer". This modified the basic layout slightly to place one of the two rest masses hanging from the end of the rod on a fiber of its own, as opposed to being attached directly to the end. This allowed it to measure torsion in two dimensions, and in turn, the local horizontal component of g. It was also much more accurate. Now generally referred to as the Eötvös balance, this device is commonly used today in prospecting by searching for local mass concentrations.

Using the new device a series of experiments taking 4000 hours was carried out with Dezsö Pekár (1873–1953) and Jenő Fekete (1880–1943) starting in 1906. These were first presented at the 16th International Geodesic Conference in London in 1909, raising the accuracy to 1 in 100 million.[4] Eötvös died in 1919, and the complete measurements were only published in 1922 by Pekár and Fekete.

Eötvös also studied similar experiments being carried out by other teams on moving ships, which led to his development of the Eötvös effect to explain the small differences they measured. These were due to the additional accelerative forces due to the motion of the ships in relation to the Earth, an effect that was demonstrated on an additional run carried out on the Black Sea in 1908.

In the 1930s a former student of Eötvös, János Renner (1889–1976), further improved the results to between 1 in 2 to 5 billion.[5] Robert H. Dicke with P. G. Roll and R. Krotkov re-ran the experiment much later using improved apparatus and further improved the accuracy to 1 in 100 billion.[6] They also made several observations about the original experiment which suggested that the claimed accuracy was somewhat suspect. Re-examining the data in light of these concerns led to an apparent very slight effect that appeared to suggest that the equivalence principle was not exact, and changed with different types of material.

In the 1980s several new physics theories attempting to combine gravitation and quantum mechanics suggested that matter and anti-matter would be affected slightly differently by gravity. Combined with Dicke's claims there appeared to be a possibility that such a difference could be measured, this led to a new series of Eötvös-type experiments (as well as timed falls in evacuated columns) that eventually demonstrated no such effect.[7][8][9][10][11][12]

A side-effect of these experiments was a re-examination of the original Eötvös data, including detailed studies of the local stratigraphy, the physical layout of the Physics Institute (which Eötvös had personally designed), and even the weather and other effects. The experiment is therefore well recorded.[13]

gollark: What are you saying "why" to‽
gollark: !time
gollark: Why what?
gollark: It would be too annoying to write that to the necessary obfuscation standards anyway.
gollark: The potatoblob does not contain any "botnet controller" stuff.

See also

References
  1. Marco Mamone Capria (2005). Physics Before and After Einstein. Amsterdam: IOS Press. p. 167. ISBN 1-58603-462-6.
  2. Brewer, Jess H. (1998). "The Eötvös Experiment".
  3. R. v. Eötvös, Mathematische und Naturwissenschaftliche Berichte aus Ungarn, 8, 65, 1890
  4. R. v. Eötvös, in Verhandlungen der 16 Allgemeinen Konferenz der Internationalen Erdmessung, G. Reiner, Berlin, 319,1910
  5. Renner, J. (1935). "KÍSÉRLETI VIZSGÁLATOK A TÖMEGVONZÁS ÉS A TEHETETLENSÉG ARÁNYOSSÁGÁRÓL" (PDF). Matematikai és Természettudományi Értesítő (in Hungarian). 53: 542–568., with abstract in German
  6. Roll, P.G; Krotkov, R; Dicke, R.H (1964). "The equivalence of inertial and passive gravitational mass". Annals of Physics. Elsevier BV. 26 (3): 442–517. Bibcode:1964AnPhy..26..442R. doi:10.1016/0003-4916(64)90259-3. ISSN 0003-4916.
  7. Fischbach, Ephraim; Sudarsky, Daniel; Szafer, Aaron; Talmadge, Carrick; Aronson, S. H. (31 March 1986). "Reanalysis of the Eötvös Experiment". Physical Review Letters. American Physical Society (APS). 56 (13): 1427. doi:10.1103/physrevlett.56.1427. ISSN 0031-9007.
  8. Thodberg, Hans Henrik (1 August 1986). "Comment on the Sign in the Reanalysis of the Eötvös Experiment". Physical Review Letters. American Physical Society (APS). 57 (9): 1192. doi:10.1103/physrevlett.57.1192.5. ISSN 0031-9007.
  9. Chu, S. Y.; Dicke, R. H. (13 October 1986). "New Force or Thermal Gradient in the Eötvös Experiment?". Physical Review Letters. American Physical Society (APS). 57 (15): 1823–1824. Bibcode:1986PhRvL..57.1823C. doi:10.1103/physrevlett.57.1823. ISSN 0031-9007.
  10. Vecsernyés, P. (15 June 1987). "Constraints on a vector coupling to baryon number from the Eötvös experiment". Physical Review D. American Physical Society (APS). 35 (12): 4018–4019. Bibcode:1987PhRvD..35.4018V. doi:10.1103/physrevd.35.4018. ISSN 0556-2821.
  11. Nordtvedt, Kenneth (15 February 1988). "Lunar laser ranging and laboratory Eötvös-type experiments". Physical Review D. American Physical Society (APS). 37 (4): 1070–1071. Bibcode:1988PhRvD..37.1070N. doi:10.1103/physrevd.37.1070. ISSN 0556-2821.
  12. Bennett, Wm. R. (23 January 1989). "Modulated-Source Eötvös Experiment at Little Goose Lock". Physical Review Letters. American Physical Society (APS). 62 (4): 365–368. Bibcode:1989PhRvL..62..365B. doi:10.1103/physrevlett.62.365. ISSN 0031-9007.
  13. Bod, L.; Fischbach, E.; Marx, G.; Náray-Ziegler, Maria (31 Aug 1990). "One Hundred Years of the Eötvös Experiment". Archived from the original on October 22, 2012.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.