Dottie number

In mathematics, the Dottie number is a constant that is the unique real root of the equation

${\displaystyle \cos x=x.}$

The Dottie number is the unique real fixed point of the cosine function

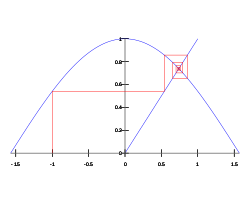
where the argument of ${\displaystyle \cos }$ is in radians. The decimal expansion of the Dottie number is ${\displaystyle 0.739085...}$.[1]

It can be trivially proved that the equation has only one solution by intermediate value theorem in the real plane. It is the single real-valued fixed point of the cosine function, and is a nontrivial example of a universal attracting fixed point. It is moreover a transcendental number as a consequence of the Lindemann-Weierstrass theorem.[2] The generalised case ${\displaystyle \cos z=z}$ for a complex variable ${\displaystyle z}$ has infinitely many roots, however unlike the Dottie number these are not attracting fixed points.

Using the Taylor series of the inverse of ${\displaystyle f(x)=\cos(x)-x}$ at ${\displaystyle {\frac {\pi }{2}}}$ (or equivalently, the Lagrange inversion theorem), the Dottie number can be expressed as the infinite series ${\displaystyle {\frac {\pi }{2}}+\sum _{n\,\mathrm {odd} }a_{n}\pi ^{n}}$ where each ${\displaystyle a_{n}}$ is a rational number defined for odd n as

${\displaystyle {\begin{aligned}a_{n}&={\frac {1}{n!2^{n}}}\lim _{m\to {\frac {\pi }{2}}}{\frac {\partial ^{n-1}}{\partial m^{n-1}}}{\left({\frac {\cos m}{m-\pi /2}}-1\right)^{-n}}\\&=-{\frac {1}{4}},-{\frac {1}{768}},-{\frac {1}{61440}},-{\frac {43}{165150720}},\ldots \end{aligned}}}$

[3][4][5][nb 1]

The name of the constant originates from Samuel Kaplan (2007) and refers to a French professor who had observed the number after repeatedly pressing the cosine button on her calculator.[3]

Notes

1. Kaplan does not give an explicit formula for the terms of the series but it follows trivially from the Lagrange inversion theorem

References

1. "OEIS A003957". oeis.org. Retrieved 2019-05-26.
2. Eric W. Weisstein. "Dottie Number".
3. Kaplan, Samuel R (February 2007). "The Dottie Number" (PDF). Mathematics Magazine. 80: 73. doi:10.1080/0025570X.2007.11953455. Retrieved 29 November 2017.
4. "OEIS A302977 Numerators of the rational factor of Kaplan's series for the Dottie number". oeis.org. Retrieved 2019-05-26.
5. "A306254 - OEIS". oeis.org. Retrieved 2019-07-22.

External links

• Miller, T. H. (Feb 1890). "On the numerical values of the roots of the equation cosx = x". Proceedings of the Edinburgh Mathematical Society. doi:10.1017/S0013091500030868.
• Salov, Valerii (2012). "Inevitable Dottie Number. Iterals of cosine and sine". arXiv:1212.1027.
• Azarian, Mohammad K. (2008). "ON THE FIXED POINTS OF A FUNCTION AND THE FIXED POINTS OF ITS COMPOSITE FUNCTIONS" (PDF). International Journal of Pure and Applied Mathematics.