Dodecahedral pyramid
In 4-dimensional geometry, the dodecahedral pyramid is bounded by one dodecahedron on the base and 12 pentagonal pyramid cells which meet at the apex. Since a dodecahedron's circumradius is greater than its edge length,[1] so the pentagonal pyramids requires tall isosceles triangle faces.
| Dodecahedral pyramid | ||
|---|---|---|
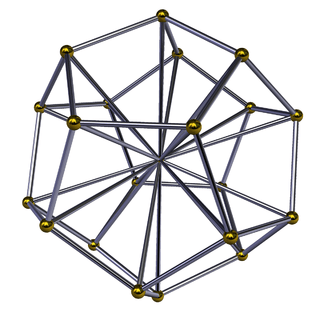 Schlegel diagram | ||
| Type | Polyhedral pyramid | |
| Schläfli symbol | ( ) ∨ {5,3} | |
| Cells | 13 | 1 {5,3} 12 ( ) ∨ {5} |
| Faces | 42 | 30 {3} 12 {5} |
| Edges | 50 | |
| Vertices | 21 | |
| Dual | icosahedral pyramid | |
| Symmetry group | H3, [5,3,1], order 120 | |
| Properties | convex | |
The dual to the dodecahedral pyramid is an icosahedral pyramid, seen as an icosahedral base, and 12 regular tetrahedral meeting at an apex.
References
- Klitzing, Richard. "3D convex uniform polyhedra o3o5x - doe". sqrt[(9+3 sqrt(5))/8] ≒ 1.401259
External links
- Olshevsky, George. "Pyramid". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.