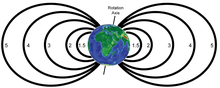
Dipole model of the Earth's magnetic field

The dipole model of the Earth's magnetic field is a first order approximation of the rather complex true Earth's magnetic field. Due to effects of the interplanetary magnetic field (IMF), and the solar wind, the dipole model is particularly inaccurate at high L-shells (e.g., above L=3), but may be a good approximation for lower L-shells. For more precise work, or for any work at higher L-shells, a more accurate model that incorporates solar effects, such as the Tsyganenko magnetic field model, is recommended.

Plot showing field lines (which, in three dimensions would describe "shells") for L-values 1.5, 2, 3, 4 and 5 using a dipole model of the Earth's magnetic field

Equations

The following equations describe the dipole magnetic field.[1]

First, define ${\displaystyle B_{0}}$ as the mean value of the magnetic field at the magnetic equator on the Earth's surface. Typically ${\displaystyle B_{0}=3.12\times 10^{-5}\ {\textrm {T}}}$.

Then, the radial and azimuthal fields can be described as

${\displaystyle B_{r}=-2B_{0}\left({\frac {R_{E}}{r}}\right)^{3}\cos \theta }$

${\displaystyle B_{\theta }=-B_{0}\left({\frac {R_{E}}{r}}\right)^{3}\sin \theta }$

${\displaystyle |B|=B_{0}\left({\frac {R_{E}}{r}}\right)^{3}{\sqrt {1+3\cos ^{2}\theta }}}$

where ${\displaystyle R_{E}}$ is the mean radius of the Earth (approximately 6370 km), ${\displaystyle r}$ is the radial distance from the center of the Earth (using the same units as used for ${\displaystyle R_{E}}$), and ${\displaystyle \theta }$ is the azimuth measured from the north magnetic pole (or geomagnetic pole).

Magnetic field components vs. latitude

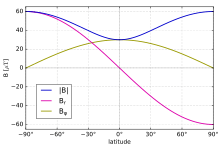
It is sometimes more convenient to express the magnetic field in terms of magnetic latitude and distance in Earth radii. The magnetic latitude (MLAT), or geomagnetic latitude, ${\displaystyle \lambda }$ is measured northwards from the equator (analogous to geographic latitude) and is related to ${\displaystyle \theta }$ by ${\displaystyle \lambda =\pi /2-\theta }$. In this case, the radial and azimuthal components of the magnetic field (the latter still in the ${\displaystyle \theta }$ direction, measured from the axis of the north pole) are given by

${\displaystyle B_{r}=-{\frac {2B_{0}}{R^{3}}}\sin \lambda }$

${\displaystyle B_{\theta }={\frac {B_{0}}{R^{3}}}\cos \lambda }$

${\displaystyle |B|={\frac {B_{0}}{R^{3}}}{\sqrt {1+3\sin ^{2}\lambda }}}$

where ${\displaystyle R}$ in this case has units of Earth radii (${\displaystyle R=r/R_{E}}$).

Invariant latitude

Invariant latitude is a parameter that describes where a particular magnetic field line touches the surface of the Earth. It is given by[2]

${\displaystyle \Lambda =\arccos \left({\sqrt {1/L}}\right)}$

or

${\displaystyle L=1/\cos ^{2}\left(\Lambda \right)}$

where ${\displaystyle \Lambda }$ is the invariant latitude and ${\displaystyle L}$ is the L-shell describing the magnetic field line in question.

On the surface of the earth, the invariant latitude (${\displaystyle \Lambda }$) is equal to the magnetic latitude (${\displaystyle \lambda }$).

See also

• Dipole
• International Geomagnetic Reference Field (IGRF)
• Magnetosphere
• World Magnetic Model (WMM)

References

1. Walt, Martin (1994). Introduction to Geomagnetically Trapped Radiation. New York, NY: Cambridge University Press. pp. 29–33. ISBN 0-521-61611-5.
2. Kivelson, Margaret; Russell, Christopher (1995). Introduction to Space Physics. New York, NY: Cambridge University Press. pp. 166–167. ISBN 0-521-45714-9.

External links

• Instant run of Tsyganenko magnetic field model from NASA CCMC
• Nikolai Tsyganenko's website including Tsyganenko model source code