Devil's curve

In geometry, a Devil's curve is a curve defined in the Cartesian plane by an equation of the form

${\displaystyle y^{2}(y^{2}-b^{2})=x^{2}(x^{2}-a^{2}).}$[1]

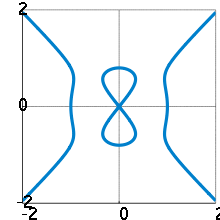
Devil's curve for a = 0.8 and b = 1.

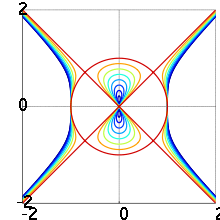
Devil's curve with ${\displaystyle a}$ ranging from 0 to 1 and b = 1 (with the curve colour going from blue to red).

Devil's curves were studied heavily by Gabriel Cramer.

The name comes from the shape its central lemniscate takes when graphed. The shape is named after the juggling game diabolo, which involves two sticks, a string, and a spinning prop in the likeness of the lemniscate. The confusion is the result of the Italian word diavolo meaning "devil".[2]

References

1. "Devil's Curve". Wolfram MathWorld.
2. Wassenaar, Jan. "devil's curve". www.2dcurves.com. Retrieved 2018-02-26.

External links

• Weisstein, Eric W. "Devil's Curve". MathWorld.
• The MacTutor History of Mathematics (University of St. Andrews) – Devil's curve