Descartes snark
In the mathematical field of graph theory, a Descartes snark is an undirected graph with 210 vertices and 315 edges. It is a snark, first discovered by William Tutte in 1948 under the pseudonym Blanche Descartes.[1]
| Descartes snark | |
|---|---|
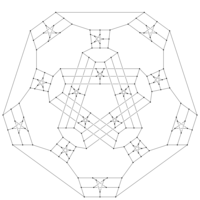 Image of a Descartes snark. | |
| Named after | Blanche Descartes |
| Vertices | 210 |
| Edges | 315 |
| Girth | 5 |
| Chromatic index | 4 |
| Properties | Cubic Snark |
| Table of graphs and parameters | |
A Descartes snark is obtained from the Petersen graph by replacing each vertex with a nonagon and each edge with a particular graph closely related to the Petersen graph. Because there are multiple ways to perform this procedure, there are multiple Descartes snarks.
Notes
- Descartes, Blanche. "Network Colorings," The Mathematical Gazette (London, 32:299. p. 67–69, 1948.
gollark: I don't think it was actually due to anything you did but just this sort of thing being really hard in general.
gollark: It probably wouldn't be. I suspect it's because it didn't really have that many people, and there was not that much actual discussion of esolangs available.
gollark: Yes, esoserver didn't work, doesn't mean you're okay.
gollark: Are, I should say.
gollark: You were *actively* very bad.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.