De Bruijn index

In mathematical logic, the de Bruijn index is a tool invented by the Dutch mathematician Nicolaas Govert de Bruijn for representing terms of lambda calculus without naming the bound variables.[1] Terms written using these indices are invariant with respect to α-conversion, so the check for α-equivalence is the same as that for syntactic equality. Each de Bruijn index is a natural number that represents an occurrence of a variable in a λ-term, and denotes the number of binders that are in scope between that occurrence and its corresponding binder. The following are some examples:

• The term λx. λy. x, sometimes called the K combinator, is written as λ λ 2 with De Bruijn indices. The binder for the occurrence x is the second λ in scope.
• The term λx. λy. λz. x z (y z) (the S combinator), with de Bruijn indices, is λ λ λ 3 1 (2 1).
• The term λz. (λy. y (λx. x)) (λx. z x) is λ (λ 1 (λ 1)) (λ 2 1). See the following illustration, where the binders are coloured and the references are shown with arrows.

This article is about a method for avoiding naming bound variables in lambda calculus. For an alternative syntax for lambda expressions, see De Bruijn notation.

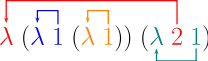
De Bruijn indices are commonly used in higher-order reasoning systems such as automated theorem provers and logic programming systems.[2]

Formal definition

Formally, λ-terms (M, N, ...) written using De Bruijn indices have the following syntax (parentheses allowed freely):

M, N, ... ::= n | M N | λ M

where n—natural numbers greater than 0—are the variables. A variable n is bound if it is in the scope of at least n binders (λ); otherwise it is free. The binding site for a variable n is the nth binder it is in the scope of, starting from the innermost binder.

The most primitive operation on λ-terms is substitution: replacing free variables in a term with other terms. In the β-reduction (λ M) N, for example, we must:

1. find the instances of the variables n₁, n₂, ..., n_k in M that are bound by the λ in λ M,
2. decrement the free variables of M to match the removal of the outer λ-binder, and
3. replace n₁, n₂, ..., n_k with N, suitably incrementing the free variables occurring in N each time, to match the number of λ-binders, under which the corresponding variable occurs when N substitutes for one of the n_i.

To illustrate, consider the application

(λ λ 4 2 (λ 1 3)) (λ 5 1)

which might correspond to the following term written in the usual notation

(λx. λy. z x (λu. u x)) (λx. w x).

After step 1, we obtain the term λ 4 □ (λ 1 □), where the variables that are destined for substitution are replaced with boxes. Step 2 decrements the free variables, giving λ 3 □ (λ 1 □). Finally, in step 3, we replace the boxes with the argument, namely λ 5 1; the first box is under one binder, so we replace it with λ 6 1 (which is λ 5 1 with the free variables increased by 1); the second is under two binders, so we replace it with λ 7 1. The final result is λ 3 (λ 6 1) (λ 1 (λ 7 1)).

Formally, a substitution is an unbounded list of term replacements for the free variables, written M₁.M₂..., where M_i is the replacement for the ith free variable. The increasing operation in step 3 is sometimes called shift and written ↑^k where k is a natural number indicating the amount to increase the variables; for example, ↑⁰ is the identity substitution, leaving a term unchanged.

The application of a substitution s to a term M is written M[s]. The composition of two substitutions s₁ and s₂ is written s₁ s₂ and defined by

M [s₁ s₂] = (M [s₁]) [s₂].

The rules for application are as follows:

${\displaystyle {\begin{aligned}n[N_{1}\ldots N_{n}\ldots ]=&N_{n}\\(M_{1}\;M_{2})[s]=&(M_{1}[s])(M_{2}[s])\\(\lambda \;M)[s]=&\lambda \;(M[1.1[s'].2[s'].3[s']\ldots ])\\&{\text{where }}s'=s\uparrow ^{1}\end{aligned}}}$

The steps outlined for the β-reduction above are thus more concisely expressed as:

(λ M) N →_β M [N.1.2.3...].

Alternatives to De Bruijn indices

When using the standard "named" representation of λ-terms, where variables are treated as labels or strings, one must explicitly handle α-conversion when defining any operation on the terms. The standard Variable Convention[3] of Barendregt is one such approach where α-conversion is applied as needed to ensure that:

1. bound variables are distinct from free variables, and
2. all binders bind variables not already in scope.

In practice this is cumbersome, inefficient, and often error-prone. It has therefore led to the search for different representations of such terms. On the other hand, the named representation of λ-terms is more pervasive and can be more immediately understandable by others because the variables can be given descriptive names. Thus, even if a system uses De Bruijn indices internally, it will present a user interface with names.

De Bruijn indices are not the only representation of λ-terms that obviates the problem of α-conversion. Among named representations, the nominal techniques of Pitts and Gabbay is one approach, where the representation of a λ-term is treated as an equivalence class of all terms rewritable to it using variable permutations.[4] This approach is taken by the Nominal Datatype Package of Isabelle/HOL.[5]

Another common alternative is an appeal to higher-order representations where the λ-binder is treated as a true function. In such representations, the issues of α-equivalence, substitution, etc. are identified with the same operations in a meta-logic.

When reasoning about the meta-theoretic properties of a deductive system in a proof assistant, it is sometimes desirable to limit oneself to first-order representations and to have the ability to name or rename assumptions. The locally nameless approach uses a mixed representation of variables—De Bruijn indices for bound variables and names for free variables—that is able to benefit from the α-canonical form of De Bruijn indexed terms when appropriate.[6][7]

See also

• The De Bruijn notation for λ-terms.
• Combinatory logic, a more essential way to eliminate variable names.

References

1. de Bruijn, Nicolaas Govert (1972). "Lambda Calculus Notation with Nameless Dummies: A Tool for Automatic Formula Manipulation, with Application to the Church-Rosser Theorem" (PDF). Indagationes Mathematicae. 34: 381–392. ISSN 0019-3577.
2. Gabbay, Murdoch J.; Pitts, Andy M. (1999). "A New Approach to Abstract Syntax Involving Binders". 14th Annual IEEE Symposium on Logic in Computer Science. pp. 214–224. doi:10.1109/LICS.1999.782617.
3. Barendregt, Henk P. (1984). The Lambda Calculus: Its Syntax and Semantics. North Holland. ISBN 978-0-444-87508-2.
4. Pitts, Andy M. (2003). "Nominal Logic: A First Order Theory of Names and Binding". Information and Computation. 186 (2): 165–193. doi:10.1016/S0890-5401(03)00138-X. ISSN 0890-5401.
5. "Nominal Isabelle web-site". Retrieved 2007-03-28.
6. McBride, McKinna. I Am Not a Number; I Am a Free Variable (PDF).
7. Aydemir, Chargueraud, Pierce, Pollack, Weirich. Engineering Formal Metatheory.CS1 maint: multiple names: authors list (link)