Cube-connected cycles

In graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by Preparata & Vuillemin (1981) for use as a network topology in parallel computing.

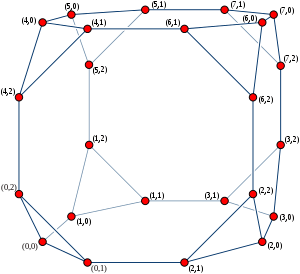
The cube-connected cycles of order 3, arranged geometrically on the vertices of a truncated cube.

Definition

The cube-connected cycles of order n (denoted CCCn) can be defined as a graph formed from a set of n2n nodes, indexed by pairs of numbers (x, y) where 0 ≤ x < 2n and 0 ≤ y < n. Each such node is connected to three neighbors: (x, (y + 1) mod n), (x, (y − 1) mod n), and (x ⊕ 2y, y), where "⊕" denotes the bitwise exclusive or operation on binary numbers.

This graph can also be interpreted as the result of replacing each vertex of an n-dimensional hypercube graph by an n-vertex cycle. The hypercube graph vertices are indexed by the numbers x, and the positions within each cycle by the numbers y.

Properties

The cube-connected cycles of order n is the Cayley graph of a group that acts on binary words of length n by rotation and flipping bits of the word.[1] The generators used to form this Cayley graph from the group are the group elements that act by rotating the word one position left, rotating it one position right, or flipping its first bit. Because it is a Cayley graph, it is vertex-transitive: there is a symmetry of the graph mapping any vertex to any other vertex.

The diameter of the cube-connected cycles of order n is 2n + ⌊n/2⌋ − 2 for any n ≥ 4; the farthest point from (x, y) is (2n − x − 1, (y + n/2) mod n).[2] Sýkora & Vrťo (1993) showed that the crossing number of CCCn is ((1/20) + o(1)) 4n.

According to the Lovász conjecture, the cube-connected cycle graph should always contain a Hamiltonian cycle, and this is now known to be true. More generally, although these graphs are not pancyclic, they contain cycles of all but a bounded number of possible even lengths, and when n is odd they also contain many of the possible odd lengths of cycles.[3]

Parallel processing application

Cube-connected cycles were investigated by Preparata & Vuillemin (1981), who applied these graphs as the interconnection pattern of a network connecting the processors in a parallel computer. In this application, cube-connected cycles have the connectivity advantages of hypercubes while only requiring three connections per processor. Preparata and Vuillemin showed that a planar layout based on this network has optimal area × time2 complexity for many parallel processing tasks.

Notes
  1. (Akers & Krishnamurthy (1989); Annexstein, Baumslag & Rosenberg (1990)).
  2. Friš, Havel & Liebl (1997).
  3. Germa, Heydemann & Sotteau (1998).
gollark: That only applies to the osmarks.net fortunes thing.
gollark: I suspect LyricLy uses a random number generator for some percentage of opinion generation.
gollark: Where you guessed *all* of them wrong (probability of about ⅓ if you picked randomly, and you claimed they were all RIGHT)?
gollark: Remember the code guessing incident?
gollark: Scripts in a browser are banned from accessing other origins which don't explicitly opt in to such, for security (as cookies are thingied, and websites may filter by IP).

References
  • Akers, Sheldon B.; Krishnamurthy, Balakrishnan (1989), "A group-theoretic model for symmetric interconnection networks", IEEE Transactions on Computers, 38 (4): 555–566, doi:10.1109/12.21148.
  • Annexstein, Fred; Baumslag, Marc; Rosenberg, Arnold L. (1990), "Group action graphs and parallel architectures", SIAM Journal on Computing, 19 (3): 544–569, doi:10.1137/0219037.
  • Friš, Ivan; Havel, Ivan; Liebl, Petr (1997), "The diameter of the cube-connected cycles", Information Processing Letters, 61 (3): 157–160, doi:10.1016/S0020-0190(97)00013-6.
  • Germa, Anne; Heydemann, Marie-Claude; Sotteau, Dominique (1998), "Cycles in the cube-connected cycles graph", Discrete Applied Mathematics, 83 (1–3): 135–155, doi:10.1016/S0166-218X(98)80001-2, MR 1622968.
  • Preparata, Franco P.; Vuillemin, Jean (1981), "The cube-connected cycles: a versatile network for parallel computation", Communications of the ACM, 24 (5): 300–309, doi:10.1145/358645.358660, hdl:2142/74219.
  • Sýkora, Ondrej; Vrťo, Imrich (1993), "On crossing numbers of hypercubes and cube connected cycles", BIT Numerical Mathematics, 33 (2): 232–237, doi:10.1007/BF01989746, hdl:11858/00-001M-0000-002D-92E4-9.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.