Cover's theorem

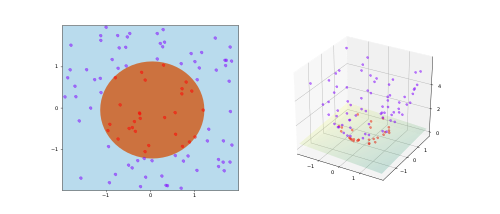
Cover's theorem is a statement in computational learning theory and is one of the primary theoretical motivations for the use of non-linear kernel methods in machine learning applications. The theorem states that given a set of training data that is not linearly separable, one can with high probability transform it into a training set that is linearly separable by projecting it into a higher-dimensional space via some non-linear transformation. The theorem is named after the information theorist Thomas M. Cover who stated it in 1965. In his own words,

A complex pattern-classification problem, cast in a high-dimensional space nonlinearly, is more likely to be linearly separable than in a low-dimensional space, provided that the space is not densely populated.

— Cover, T.M., Geometrical and Statistical properties of systems of linear inequalities with applications in pattern recognition, 1965

Proof

A deterministic mapping may be used: suppose there are ${\displaystyle n}$ samples. Lift them onto the vertices of the simplex in the ${\displaystyle n-1}$ dimensional real space. Since every partition of the samples into two sets is separable by a linear separator, the theorem follows.

The left image shows 100 samples in the two dimensional real space. These samples are not linearly separable, but lifting the samples to the three dimensional space with the kernel trick, the samples becomes linearly separable. Note that in this case and in many other cases will not be necessary to lift the samples to the 100 dimensional space as in the proof of theorem.

References

• Haykin, Simon (2009). Neural Networks and Learning Machines (Third ed.). Upper Saddle River, New Jersey: Pearson Education Inc. pp. 232–236. ISBN 978-0-13-147139-9.
• Cover, T.M. (1965). "Geometrical and Statistical properties of systems of linear inequalities with applications in pattern recognition" (PDF). IEEE Transactions on Electronic Computers. EC-14 (3): 326–334. doi:10.1109/pgec.1965.264137.
• Mehrotra, K.; Mohan, C. K.; Ranka, S. (1997). Elements of artificial neural networks (2nd ed.). MIT Press. ISBN 0-262-13328-8. (Section 3.5)

See also

• Kernel method