Couette flow

In fluid dynamics, Couette flow is the flow of a viscous fluid in the space between two surfaces, one of which is moving tangentially relative to the other. The configuration often takes the form of two parallel plates or the gap between two concentric cylinders. The flow is driven by virtue of viscous drag force acting on the fluid, but may additionally be motivated by an applied pressure gradient in the flow direction. The Couette configuration models certain practical problems, like flows in the Earth's mantle and the atmosphere[1], flow in lightly loaded journal bearings, and is often employed in viscometry and to demonstrate approximations of reversibility.[2] This type of flow is named in honor of Maurice Couette, a Professor of Physics at the French University of Angers in the late 19th century.

Planar Couette flow

Simple Couette configuration using two infinite flat plates.

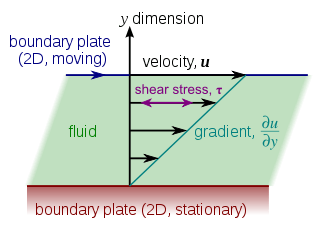
Couette flow is frequently used in undergraduate physics and engineering courses to illustrate shear-driven fluid motion. The simplest conceptual configuration finds two infinite, parallel plates separated by a distance ${\displaystyle h}$. One plate, say the top one, translates with a constant velocity ${\displaystyle U}$ in its own plane. Neglecting pressure gradients, the Navier–Stokes equations simplify to

${\displaystyle {\frac {d^{2}u}{dy^{2}}}=0,}$

where ${\displaystyle y}$ is a spatial coordinate normal to the plates and ${\displaystyle u(y)}$ is the velocity distribution. This equation reflects the assumption that the flow is uni-directional. That is, only one of the three velocity components ${\displaystyle (u,v,w)}$ is non-trivial. If y originates at the lower plate, the boundary conditions are ${\displaystyle u(0)=0}$ and ${\displaystyle u(h)=U}$. The exact solution

${\displaystyle u(y)=U{\frac {y}{h}}}$

can be found by integrating twice and solving for the constants using the boundary conditions. A notable aspect of the flow is that shear stress is constant throughout the flow domain.[3] In particular, the first derivative of the velocity, ${\displaystyle U/h}$, is constant. (This is implied by the straight-line profile in the figure.) According to Newton's Law of Viscosity (Newtonian fluid), the shear stress is the product of this expression and the (constant) fluid viscosity.

Startup of Couette flow[4][5]

Startup Couette flow

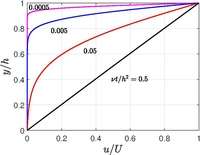
In reality, the Couette solution cannot be reached instantaneously. The startup problem is given by

${\displaystyle {\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}}$

subject to the initial condition

${\displaystyle u(y,0)=0,\quad 0<y<h,}$

with boundary conditions (same as Couette flow)

${\displaystyle u(0,t)=0,\quad u(h,t)=U,\quad t>0.}$

The problem can be converted to a homogeneous problem by subtracting steady solution and using separation of variables, the solution is given by

${\displaystyle u(y,t)=U{\frac {y}{h}}-{\frac {2U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{n}}e^{-n^{2}\pi ^{2}\nu t/h^{2}}\sin \left[n\pi \left(1-{\frac {y}{h}}\right)\right]}$.

As ${\displaystyle t\rightarrow \infty }$, the steady Couette solution is recovered. At times ${\displaystyle t\sim h^{2}/\nu }$, steady Couette solution will be almost reached as shown in the figure. The time required to reach the steady solution depends only on the spacing between the plates ${\displaystyle h}$ and the kinematic viscosity of the fluid, but not on how fast the top plate is moved ${\displaystyle U}$.

Couette flow with pressure gradient[6]

A more general Couette flow situation arises when a constant pressure gradient ${\displaystyle G=-dp/dx=\mathrm {constant} }$ is imposed in a direction parallel to the plates. This problem was studied by H. S. Rowell and U. D. Finlayson[7][8]. The Navier–Stokes equations, in this case, simplify to

${\displaystyle {\frac {d^{2}u}{dy^{2}}}=-{\frac {G}{\mu }},}$

where ${\displaystyle \mu }$ is fluid viscosity. Integrating the above equation twice and applying the boundary conditions (same as in the case of Couette flow without pressure gradient) to yield the following exact solution

${\displaystyle u(y)={\frac {G}{2\mu }}y(h-y)+U{\frac {y}{h}}.}$

The pressure gradient can be positive (adverse pressure gradient) or negative (favorable pressure gradient). It may be noted that in the limiting case of stationary plates(${\displaystyle U=0}$), the flow is referred to as Plane Poiseuille flow with a symmetric (with reference to the horizontal mid-plane) parabolic velocity profile.

Compressible plane Couette flow

Compressible Couette flow for M=0

Compressible Couette flow for M^2Pr=7.5

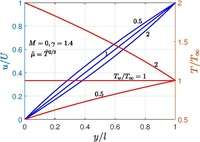
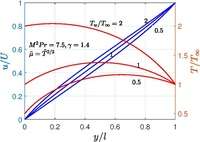
This problem was first addressed by C.R. Illingworth[9] in 1950. In incompressible flow, the velocity profile is linear because the fluid temperature is constant. When the upper and lower walls are maintained at different temperatures, the velocity profile is complicated, but it turns out it has an exact implicit solution.

Consider the plane Couette flow[10] with lower wall at rest and fluid properties being denoted with subscript ${\displaystyle w}$ and let the upper wall move with constant velocity ${\displaystyle U}$ with properties denoted with subscript ${\displaystyle \infty }$. The properties and the pressure at the upper wall are prescribed and taken as reference quantities. Let ${\displaystyle l}$ be the distance between the two walls. The boundary conditions are

${\displaystyle u=0,\ v=0,\ h=h_{w}=c_{pw}T_{w}\ {\text{at}}\ y=0,}$

${\displaystyle u=U,\ v=0,\ h=h_{\infty }=c_{p\infty }T_{\infty },\ p=p_{\infty }\ {\text{at}}\ y=l}$

where ${\displaystyle h}$ is the specific enthalpy and ${\displaystyle c_{p}}$ is the specific heat. Conservation of mass and ${\displaystyle y}$ momentum reveals that ${\displaystyle v=0,\ p=p_{\infty }}$ everywhere in the flow domain. Conservation of ${\displaystyle x}$ momentum and energy reduce to

${\displaystyle {\frac {d}{dy}}\left(\mu {\frac {du}{dy}}\right)=0,\quad \Rightarrow \quad {\frac {d\tau }{dy}}=0,\quad \Rightarrow \quad \tau =\tau _{w}}$

${\displaystyle {\frac {1}{Pr}}{\frac {d}{dy}}\left(\mu {\frac {dh}{dy}}\right)+\mu \left({\frac {du}{dy}}\right)^{2}=0.}$

where ${\displaystyle \tau =\tau _{w}={\text{constant}}}$ is the wall shear stress, but the whole flow domain takes the same shear stress similar to the incompressible Couette flow. The flow does not depend on the Reynolds number ${\displaystyle Re=Ul/\nu _{\infty }}$, but rather on the Prandtl number ${\displaystyle Pr=\mu _{\infty }c_{p\infty }/\kappa _{\infty }}$ and the Mach number ${\displaystyle M=U/c_{\infty }=U/{\sqrt {(\gamma -1)h_{\infty }}}}$, where ${\displaystyle \kappa }$ is the thermal conductivity, ${\displaystyle c}$ is the Speed of sound and ${\displaystyle \gamma }$ is the Specific heat ratio. It turns out that the said problem can be solved implicitly. Introduce the non-dimensional variables

${\displaystyle {\tilde {y}}={\frac {y}{l}},\quad {\tilde {T}}={\frac {T}{T_{\infty }}},\quad {\tilde {T}}_{w}={\frac {T_{w}}{T_{\infty }}},\quad {\tilde {h}}={\frac {h}{h_{\infty }}},\quad {\tilde {h}}_{w}={\frac {h_{w}}{h_{\infty }}},\quad {\tilde {u}}={\frac {u}{U}},\quad {\tilde {\mu }}={\frac {\mu }{\mu _{\infty }}},\quad {\tilde {\tau }}_{w}={\frac {\tau _{w}}{\mu _{\infty }U/l}}}$

Therefore, the solutions are

${\displaystyle {\tilde {h}}={\tilde {h}}_{w}+\left[{\frac {\gamma -1}{2}}M^{2}Pr+(1-{\tilde {h}}_{w})\right]{\tilde {u}}-{\frac {\gamma -1}{2}}M^{2}Pr{\tilde {u}}^{2},}$

${\displaystyle {\tilde {y}}={\frac {1}{{\tilde {\tau }}_{w}}}\int _{0}^{\tilde {u}}{\tilde {\mu }}d{\tilde {u}},\quad {\tilde {\tau }}_{w}=\int _{0}^{1}{\tilde {\mu }}d{\tilde {u}},\quad q_{w}=-{\frac {1}{Pr}}\tau _{w}\left({\frac {dh}{du}}\right)_{w},}$

${\displaystyle q_{w}}$ is the heat transferred per unit time per unit area from the lower wall. Thus ${\displaystyle {\tilde {h}},{\tilde {T}},{\tilde {u}},{\tilde {\mu }}}$ are implicit functions of ${\displaystyle y}$. It is useful to write the solution in terms of recovery temperature ${\displaystyle T_{r}}$ and recovery enthalpy ${\displaystyle h_{r}}$ as the temperature of an insulated wall i.e., the value of ${\displaystyle T_{w},\ h_{w}}$ for which ${\displaystyle q_{w}=0}$. Then the solution is

${\displaystyle {\frac {q_{w}}{\tau _{w}U}}={\frac {{\tilde {T}}_{w}-{\tilde {T}}_{r}}{(\gamma -1)M^{2}Pr}},\quad {\tilde {T}}_{r}=1+{\frac {\gamma -1}{2}}M^{2}Pr,}$

${\displaystyle {\tilde {h}}={\tilde {h}}_{w}+({\tilde {h}}_{r}-{\tilde {h}}_{w}){\tilde {u}}-{\frac {\gamma -1}{2}}M^{2}Pr{\tilde {u}}^{2}.}$

If specific heat is assumed constant, then ${\displaystyle {\tilde {h}}={\tilde {T}}}$. When ${\displaystyle M\rightarrow 0}$ and ${\displaystyle T_{w}=T_{\infty },\Rightarrow q_{w}=0}$, then ${\displaystyle T}$ and ${\displaystyle \mu }$ are constant everywhere, thus recovering the incompressible Couette flow solution. Except this case, one should know ${\displaystyle {\tilde {\mu }}({\tilde {T}})}$ to solve the problem. When ${\displaystyle M\rightarrow 0}$ and ${\displaystyle q_{w}\neq 0}$, the recovery quantities become unity ${\displaystyle {\tilde {T}}_{r}=1}$. There are number of laws to predict ${\displaystyle {\tilde {\mu }}({\tilde {T}}),}$ for example Sutherland's formula, power law etc. For air, the values of ${\displaystyle \gamma =1.4,\ {\tilde {\mu }}({\tilde {T}})={\tilde {T}}^{2/3}}$ are commonly used and the results for this case is shown in figure.

Liepmann[11][12] studied the effects of dissociation and ionization (i.e. ${\displaystyle c_{p}}$ is not constant) and showed that the recovery temperature is reduced by the dissociation of molecules and also he studied the hydromagnetics[13] effects on this compressible Couette flow.

Couette flow in rectangular channel

Couette flow for square channel

Couette flow with h/l=0.1

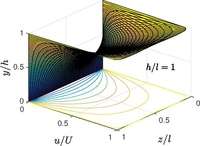
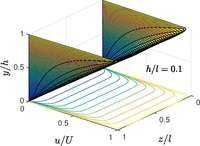
One-dimensional flow ${\displaystyle u(y)}$ is valid when both plates are infinitely long in streamwise ${\displaystyle x}$ and spanwise ${\displaystyle z}$ direction. When the spanwise length is made finite, the flow becomes two-dimensional ${\displaystyle u(y,z)}$. The infinitely long length in streamwise direction still needs to be held to ensure the uni-directional nature of the flow.
The below problem is due to Rowell and Finlayson (1928).[14] Consider an infinitely long rectangular channel with transverse height ${\displaystyle h}$ and spanwise width ${\displaystyle l}$, subjected to the condition that the top wall moves with a constant velocity ${\displaystyle U}$. Without any imposed pressure gradient, the Navier–Stokes equations reduce to

${\displaystyle {\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=0}$

with boundary conditions

${\displaystyle u(0,z)=0,\quad u(h,z)=U,}$

${\displaystyle u(y,0)=0,\quad u(y,l)=0.}$

Using separation of variables, the solution is given by

${\displaystyle u(y,z)={\frac {4U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {\sinh(\beta _{n}y)}{\sinh(\beta _{n}h)}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}}.}$

When ${\displaystyle h/l<<1}$, the classical plane Couette is recovered as shown in the figure.

Couette flow between coaxial cylinders

Couette flow between coaxial cylinders[15] also known as Taylor–Couette flow is a flow created between two rotating infinitely long co-axial cylinders. The original problem was solved by Stokes in 1845,[16] but Geoffrey Ingram Taylor's name was attached to the flow because he studied the stability of the flow in his famous paper[17] in 1923. If the inner cylinder with radius ${\displaystyle R_{1}}$ is rotating at a constant angular velocity ${\displaystyle \Omega _{1}}$ and the outer cylinder with radius ${\displaystyle R_{2}}$ is rotating at a constant angular velocity ${\displaystyle \Omega _{2}}$, then the velocity in ${\displaystyle \theta }$ direction is given by

${\displaystyle v_{\theta }(r)=ar+{\frac {b}{r}},\qquad a={\frac {\Omega _{2}R_{2}^{2}-\Omega _{1}R_{1}^{2}}{R_{2}^{2}-R_{1}^{2}}},\quad b={\frac {(\Omega _{1}-\Omega _{2})R_{1}^{2}R_{2}^{2}}{R_{2}^{2}-R_{1}^{2}}}.}$

(Note that r has replaced y in this result to reflect cylindrical rather than rectangular coordinates). It is clear from this equation that curvature effects no longer allow for constant shear in the flow domain, as shown above.

Couette flow between coaxial cylinders of finite length

The classical Taylor–Couette flow problem assumes infinitely long cylinders, but the finite-length effects which are encountered in real life are more pronounced in cylindrical geometry. The flow is still unidirectional and the solution for ${\displaystyle \Omega _{2}=0}$ with cylinder length ${\displaystyle l}$ using separation of variables or using integral transforms is given by[18]

${\displaystyle v_{\theta }(r,z)={\frac {4R_{1}\Omega _{1}}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}r)-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}r)}{I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}R_{1})-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}R_{1})}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}},}$

where ${\displaystyle I(\beta _{n}r),\ K(\beta _{n}r)}$ are Modified Bessel function of the first kind and Modified Bessel function of the second kind respectively.

See also

• Stokes-Couette flow
• Hagen–Poiseuille equation
• Taylor–Couette flow
• Hagen–Poiseuille flow from the Navier–Stokes equations

References

1. Zhilenko D., Krivonosova O., Gritsevich M., Read P. (2018) Wave number selection in the presence of noise: experimental results. Chaos: An Interdisciplinary Journal of Nonlinear Science 28, 053110 https://doi.org/10.1063/1.5011349
2. J. P. Heller (1960) "An unmixing demonstration" American Journal of Physics 28, 348-353.
3. Kundu P and Cohen I. Fluid Mechanics.
4. Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.
5. Acheson, David J. Elementary fluid dynamics. Oxford University Press, 1990.
6. George Keith Batchelor, . An introduction to fluid dynamics. Cambridge university press, 2000.
7. Rowell, H. S. (1928). U. D. Finlayson. Engineering 17, 606 (1922), 23, 249.
8. Bateman, H. (1932). Partial differential equations of mathematical physics. Partial Differential Equations of Mathematical Physics, by H. Bateman, Cambridge, UK: Cambridge University Press, 1932. pp. 175
9. Illingworth, C. R. "Some solutions of the equations of flow of a viscous compressible fluid." Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 46. No. 03. Cambridge University Press, 1950.
10. Paco Lagerstrom. Laminar flow theory. Princeton University Press, 1996.
11. Liepmann, Hans Wolfgang, and Anatol Roshko. Elements of gasdynamics. Courier Corporation, 1957.
12. Liepmann, H. W., and Z. O. Bleviss. "The effects of dissociation and ionization on compressible couette flow." Douglas Aircraft Co. Rept. SM-19831 130 (1956).
13. Liepmann, H. W. "Hydromagnetic effects in Couette and Stokes flow." The Plasma in a Magnetic Field: A Symposium. Stanford University Press, 1958.
14. Rowell, H. S. "u. D. Finlayson." Engineering 17, 606 (1922) 23 (1928): 249.
15. Lev Landau and E. M. Lifshitz. "Fluid Mechanics Pergamon." New York 61 (1959).
16. G. G. Stokes (1845) ``On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids, in Mathematical and Physical Papers, pp. 102-104, Cambridge, UK: Cambridge University Press, 1880.
17. G. I. Taylor (1923) "Stability of a Viscous Liquid Contained between Two Rotating Cylinders", Philosophical Transactions of the Royal Society of London. Series A 223, 289–343.
18. Wendl, Michael C. "General solution for the Couette flow profile." Physical Review E 60.5 (1999): 6192.

• Richard Feynman (1964) The Feynman Lectures on Physics: Mainly Electromagnetism and Matter, § 41–6 "Couette flow", Addison–Wesley ISBN 0-201-02117-X .

External links

• AMS Glossary: Couette Flow
• A rheologists perspective: the science behind the couette cell accessory