Cottrell atmosphere

In materials science, the concept of the Cottrell atmosphere was introduced by A. H. Cottrell and B. A. Bilby in 1949[1] to explain how dislocations are pinned in some metals by boron, carbon, or nitrogen interstitials.

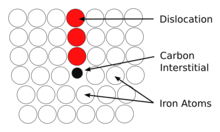
A carbon atom below a dislocation in iron, forming a Cottrell atmosphere

Cottrell atmospheres occur in body-centered cubic (BCC) and face-centered cubic (FCC) materials, such as iron or nickel, with small impurity atoms, such as boron[2], carbon,[3] or nitrogen. As these interstitial atoms distort the lattice slightly, there will be an associated residual stress field surrounding the interstitial. This stress field can be relaxed by the interstitial atom diffusing towards a dislocation, which contains a small gap at its core (as it is a more open structure), see Figure 1. Once the atom has diffused into the dislocation core the atom will stay. Typically only one interstitial atom is required per lattice plane of the dislocation.

Once a dislocation has become pinned, a large force is required to unpin the dislocation prior the yielding, thus at room temperature, the dislocation will not get unpinned.[4] This produces an observed upper yield point in a stress–strain graph. Beyond the upper yield point, the pinned dislocation will act as Frank–Read source to generate new dislocations that are not pinned. These dislocations are free to move in the crystal, which results in a subsequent lower yield point, and the material will deform in a more plastic manner.

Leaving the sample to age, by holding it at room temperature for a few hours, enables the carbon atoms to rediffuse back to dislocation cores, resulting in a return of the upper yield point.

Cottrell atmospheres lead to formation of Lüders bands and large forces for deep drawing and forming large sheets, making them a hindrance to manufacture. Some steels are designed to remove the Cottrell atmosphere effect by removing all the interstitial atoms. Steels such as interstitial free steel are decarburized and small quantities of titanium are added to remove nitrogen.


Similar phenomena

While the Cottrell atmosphere is a general effect, there are additional related mechanisms that occur under more specialized circumstances.

Suzuki effect

The Suzuki effect is characterized by the segregation of solutes to stacking fault defects. When dislocations in an FCC system split into two partial dislocations, a hexagonal close-packed (HCP) stacking fault is formed between the two partials. H. Suzuki predicted that the concentration of solute atoms at this boundary would differ from the bulk. Moving through this field of solute atoms would therefore produce a similar drag on dislocations as the Cottrell atmosphere. [5] Suzuki later observed such segregation in 1961. [6] 

Snoek effect

The Snoek effect is characterized by the ordering of solute atoms in a dislocation stress field. In BCC metals, interstitial sites of an unstrained lattice are equally favorable. However, once a strain is applied on the lattice, such as that formed by a dislocation, 1/3 of the sites become more favorable than the other 2/3. Solute atoms will therefore move to occupy the favorable sites, forming an short ranged order of solutes immediately within the vicinity of the dislocation.[7] More energy is therefore required to break a dislocation from this order.

gollark: 🌵
gollark: || ||
gollark: ||'||
gollark: ||·||
gollark: ||'||

References
  1. Cottrell, A. H.; Bilby, B. A. (1949), "Dislocation Theory of Yielding and Strain Ageing of Iron", Proceedings of the Physical Society, 62 (1): 49–62, Bibcode:1949PPSA...62...49C, doi:10.1088/0370-1298/62/1/308
  2. Blavette, D.; Cadel, E.; Fraczkiewicz, A.; Menand, A. (1999). "Three-Dimensional Atomic-Scale Imaging of Impurity Segregation to Line Defects". Science. 286 (5448): 2317–2319. doi:10.1126/science.286.5448.2317. PMID 10600736.
  3. Waseda, Osamu; Veiga, Roberto GA; Morthomas, Julien; Chantrenne, Patrice; Becquart, Charlotte S.; Ribeiro, Fabienne; Jelea, Andrei; Goldenstein, Helio; Perez, Michel (March 2017). "Formation of carbon Cottrell atmospheres and their effect on the stress field around an edge dislocation". Scripta Materialia. 129: 16–19. doi:10.1016/j.scriptamat.2016.09.032. ISSN 1359-6462.
  4. Veiga, R.G.A.; Goldenstein, H.; Perez, M.; Becquart, C.S. (1 November 2015). "Monte Carlo and molecular dynamics simulations of screw dislocation locking by Cottrell atmospheres in low carbon Fe–C alloys". Scripta Materialia. 108: 19–22. doi:10.1016/j.scriptamat.2015.06.012. ISSN 1359-6462.
  5. Suzuki, Hideji (1952-01-01). "Chemical Interaction of Solute Atoms with Dislocations". Science Reports of the Research Institutes, Tohoku University. Ser. A, Physics, Chemistry and Metallurgy (in Japanese). 4: 455–463.
  6. Suzuki, Hideji (1962-02-15). "Segregation of Solute Atoms to Stacking Faults". Journal of the Physical Society of Japan. 17 (2): 322–325. Bibcode:1962JPSJ...17..322S. doi:10.1143/JPSJ.17.322. ISSN 0031-9015.
  7. Hosford, William F. (2005). Mechanical behavior of materials. Cambridge: Cambridge University Press. ISBN 0-521-84670-6. OCLC 56482243.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.