Convex combination

In convex geometry, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1.[1]

Given three points ${\displaystyle x_{1},x_{2},x_{3}}$ in a plane as shown in the figure, the point ${\displaystyle P}$ is a convex combination of the three points, while ${\displaystyle Q}$ is not.

(${\displaystyle Q}$ is however an affine combination of the three points, as their affine hull is the entire plane.)

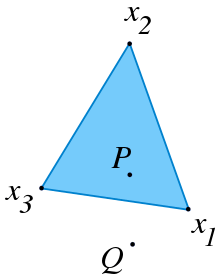
More formally, given a finite number of points ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ in a real vector space, a convex combination of these points is a point of the form

${\displaystyle \alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}$

where the real numbers ${\displaystyle \alpha _{i}}$ satisfy ${\displaystyle \alpha _{i}\geq 0}$ and ${\displaystyle \alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}=1.}$[1]

As a particular example, every convex combination of two points lies on the line segment between the points.[1]

A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical to the set of all their convex combinations.[1]

There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval ${\displaystyle [0,1]}$ is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distributions, as linear combinations preserve neither nonnegativity nor affinity (i.e., having total integral one).

Other objects

• Similarly, a convex combination ${\displaystyle X}$ of probability distributions ${\displaystyle Y_{i}}$ is a weighted sum (where ${\displaystyle \alpha _{i}}$ satisfy the same constraints as above) of its component probability distributions, often called a finite mixture distribution, with probability density function:

${\displaystyle f_{X}(x)=\sum _{i=1}^{n}\alpha _{i}f_{Y_{i}}(x)}$

Related constructions

Further information: Linear combination § Affine, conical, and convex combinations

• A conical combination is a linear combination with nonnegative coefficients. When a point ${\displaystyle x}$ is to be used as the reference origin for defining displacement vectors, then ${\displaystyle x}$ is a convex combination of ${\displaystyle n}$ points ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ if and only if the zero displacement is a non-trivial conical combination of their ${\displaystyle n}$ respective displacement vectors relative to ${\displaystyle x}$.
• Weighted means are functionally the same as convex combinations, but they use a different notation. The coefficients (weights) in a weighted mean are not required to sum to 1; instead the weighted linear combination is explicitly divided by the count of the weights.
• Affine combinations are like convex combinations, but the coefficients are not required to be non-negative. Hence affine combinations are defined in vector spaces over any field.

See also

• Affine hull
• Carathéodory's theorem (convex hull)
• Simplex
• Barycentric coordinate system

References

1. Rockafellar, R. Tyrrell (1970), Convex Analysis, Princeton Mathematical Series, 28, Princeton University Press, Princeton, N.J., pp. 11–12, MR 0274683