Conchoid of de Sluze

The conchoid(s) of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.[1]

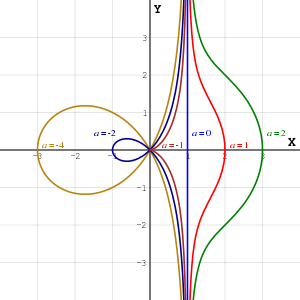
The Conchoid of de Sluze for several values of a

The curves are defined by the polar equation

${\displaystyle r=\sec \theta +a\cos \theta \,}$.

In cartesian coordinates, the curves satisfy the implicit equation

${\displaystyle (x-1)(x^{2}+y^{2})=ax^{2}\,}$

except that for a=0 the implicit form has an acnode (0,0) not present in polar form.

They are rational, circular, cubic plane curves.

These expressions have an asymptote x=1 (for a≠0). The point most distant from the asymptote is (1+a,0). (0,0) is a crunode for a<−1.

The area between the curve and the asymptote is, for ${\displaystyle a\geq -1}$,

${\displaystyle |a|(1+a/4)\pi \,}$

while for ${\displaystyle a<-1}$, the area is

${\displaystyle \left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}-a\left(2+{\frac {a}{2}}\right)\arcsin {\frac {1}{\sqrt {-a}}}.}$

If ${\displaystyle a<-1}$, the curve will have a loop. The area of the loop is

${\displaystyle \left(2+{\frac {a}{2}}\right)a\arccos {\frac {1}{\sqrt {-a}}}+\left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}.}$

Four of the family have names of their own:

a=0, line (asymptote to the rest of the family)

a=−1, cissoid of Diocles

a=−2, right strophoid

a=−4, trisectrix of Maclaurin

References

1. Smith, David Eugene (1958), History of Mathematics, Volume 2, Courier Dover Publications, p. 327, ISBN 9780486204307.