Compound of ten triangular prisms

This uniform polyhedron compound is a chiral symmetric arrangement of 10 triangular prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.

Compound of ten triangular prisms

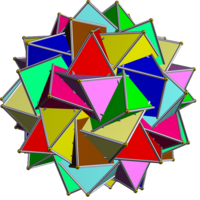Type	Uniform compound
Index	UC₃₂
Polyhedra	10 triangular prisms
Faces	20 triangles, 30 squares
Edges	90
Vertices	60
Symmetry group	chiral icosahedral (I)
Subgroup restricting to one constituent	3-fold dihedral (D₃)

Related polyhedra

This compound shares its vertex arrangement with three uniform polyhedra as follows:

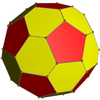convex hull	Rhombidodecadodecahedron	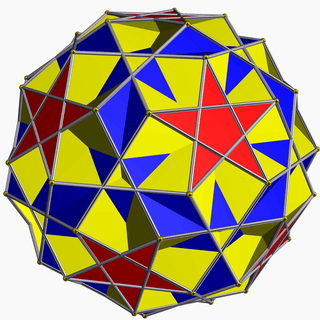Icosidodecadodecahedron
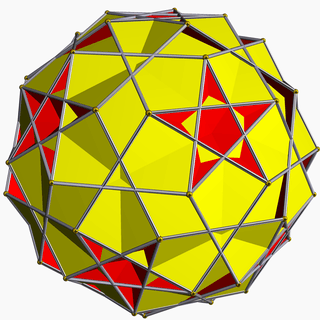Rhombicosahedron	Compound of ten triangular prisms	Compound of twenty triangular prisms

gollark: Basically, what this does is iterate over all peripheral names, check if they're the type you want, and add them to the table if they are.

gollark: *Why* do you want that, exactly?

gollark: ```lualocal monitor_names = {}for _, n in pairs(peripheral.getNames()) do if peripheral.getType(n) == "monitor" then table.insert(monitor_names, n) endend```

gollark: If you want the *names* for whatever reason, that is somewhat harder.

gollark: It has multiple returns, so do `{peripheral.find "monitor"}` if you want a table of all monitors.

References

Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.