Compound of five truncated cubes
This uniform polyhedron compound is a composition of 5 truncated cubes, formed by truncating each of the cubes in the compound of 5 cubes.
| Compound of five truncated cubes | |
|---|---|
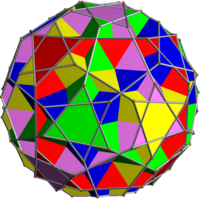 | |
| Type | Uniform compound |
| Index | UC57 |
| Polyhedra | 5 truncated cubes |
| Faces | 40 triangles, 30 octagons |
| Edges | 180 |
| Vertices | 120 |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the cyclic permutations of
- (±(2+√2), ±√2, ±(2+√2))
- (±τ, ±(τ−1+τ−1√2), ±(2τ−1+τ√2))
- (±1, ±(τ−2−τ−1√2), ±(τ2+τ√2))
- (±(1+√2), ±(−τ−2−√2), ±(τ2+√2))
- (±(τ+τ√2), ±(−τ−1), ±(2τ−1+τ−1√2))
where τ = (1+√5)/2 is the golden ratio (sometimes written φ).
gollark: This is the e-ink version.
gollark: No, that's on the Android-running Kindles.
gollark: If you're worried about ethics, stop being that, as it is ethical.
gollark: This results in generation of 3333333333333333333333333333333333333333333 capital.
gollark: Basically, they fire arbitrary items to populated ground locations, and then retroactively edit things such that someone bought them.
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (03): 447–457, doi:10.1017/S0305004100052440, MR 0397554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.