Compound of five icosahedra

The compound of five icosahedra is uniform polyhedron compound. It's composed of 5 icosahedra, rotated around a common axis. It has icosahedral symmetry I_h.

Compound of five icosahedra
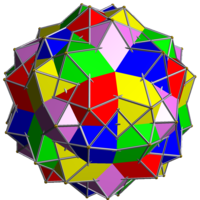Type	Uniform compound
Index	UC47
Polyhedra	5 icosahedra
Faces	40+60 Triangles
Edges	150
Vertices	60
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	pyritohedral (Th)

3D model of a compound of five icosahedra

The triangles in this compound decompose into two orbits under action of the symmetry group: 40 of the triangles lie in coplanar pairs in icosahedral planes, while the other 60 lie in unique planes.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the cyclic permutations of

(0, ±2, ±2τ)

(±τ⁻¹, ±1, ±(1+τ²))

(±τ, ±τ², ±(2τ−1))

where τ = (1+√5)/2 is the golden ratio (sometimes written φ).

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.