Cofunction

In mathematics, a function f is cofunction of a function g if f(A) = g(B) whenever A and B are complementary angles.[1] This definition typically applies to trigonometric functions.[2][3] The prefix "co-" can be found already in Edmund Gunter's Canon triangulorum (1620).[4][5]

This article is about trigonometric functions. For the computer program components, see Coroutine.

For other uses of the prefix "co" in mathematics, see dual (category theory).

Sine and cosine are each other's cofunctions.

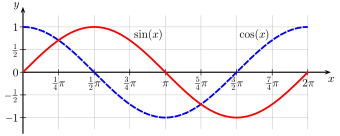
For example, sine (Latin: sinus) and cosine (Latin: cosinus,[4][5] sinus complementi[4][5]) are cofunctions of each other (hence the "co" in "cosine"):

${\displaystyle \sin \left({\frac {\pi }{2}}-A\right)=\cos(A)}$[1][3]	${\displaystyle \cos \left({\frac {\pi }{2}}-A\right)=\sin(A)}$[1][3]

The same is true of secant (Latin: secans) and cosecant (Latin: cosecans, secans complementi) as well as of tangent (Latin: tangens) and cotangent (Latin: cotangens,[4][5] tangens complementi[4][5]):

${\displaystyle \sec \left({\frac {\pi }{2}}-A\right)=\csc(A)}$[1][3]	${\displaystyle \csc \left({\frac {\pi }{2}}-A\right)=\sec(A)}$[1][3]
${\displaystyle \tan \left({\frac {\pi }{2}}-A\right)=\cot(A)}$[1][3]	${\displaystyle \cot \left({\frac {\pi }{2}}-A\right)=\tan(A)}$[1][3]

These equations are also known as the cofunction identities.[2][3]

This also holds true for the versine (versed sine, ver) and coversine (coversed sine, cvs), the vercosine (versed cosine, vcs) and covercosine (coversed cosine, cvc), the haversine (half-versed sine, hav) and hacoversine (half-coversed sine, hcv), the havercosine (half-versed cosine, hvc) and hacovercosine (half-coversed cosine, hcc), as well as the exsecant (external secant, exs) and excosecant (external cosecant, exc):

${\displaystyle \operatorname {ver} \left({\frac {\pi }{2}}-A\right)=\operatorname {cvs} (A)}$[6]	${\displaystyle \operatorname {cvs} \left({\frac {\pi }{2}}-A\right)=\operatorname {ver} (A)}$
${\displaystyle \operatorname {vcs} \left({\frac {\pi }{2}}-A\right)=\operatorname {cvc} (A)}$[7]	${\displaystyle \operatorname {cvc} \left({\frac {\pi }{2}}-A\right)=\operatorname {vcs} (A)}$
${\displaystyle \operatorname {hav} \left({\frac {\pi }{2}}-A\right)=\operatorname {hcv} (A)}$	${\displaystyle \operatorname {hcv} \left({\frac {\pi }{2}}-A\right)=\operatorname {hav} (A)}$
${\displaystyle \operatorname {hvc} \left({\frac {\pi }{2}}-A\right)=\operatorname {hcc} (A)}$	${\displaystyle \operatorname {hcc} \left({\frac {\pi }{2}}-A\right)=\operatorname {hvc} (A)}$
${\displaystyle \operatorname {exs} \left({\frac {\pi }{2}}-A\right)=\operatorname {exc} (A)}$	${\displaystyle \operatorname {exc} \left({\frac {\pi }{2}}-A\right)=\operatorname {exs} (A)}$

See also

• Hyperbolic cosine
• Hyperbolic cosecant
• Hyperbolic cotangent
• Lemniscatic cosine
• Jacobi elliptic cosine
• Cologarithm
• Covariance
• List of trigonometric identities

References

1. Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). "Chapter II. The Acute Angle [10] Functions of complementary angles". Trigonometry. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company. pp. 11–12.
2. Aufmann, Richard; Nation, Richard (2014). Algebra and Trigonometry (8 ed.). Cengage Learning. p. 528. ISBN 978-128596583-3. Retrieved 2017-07-28.
3. Bales, John W. (2012) [2001]. "5.1 The Elementary Identities". Precalculus. Archived from the original on 2017-07-30. Retrieved 2017-07-30.
4. Gunter, Edmund (1620). Canon triangulorum.
5. Roegel, Denis, ed. (2010-12-06). "A reconstruction of Gunter's Canon triangulorum (1620)" (Research report). HAL. inria-00543938. Archived from the original on 2017-07-28. Retrieved 2017-07-28.
6. Weisstein, Eric Wolfgang. "Coversine". MathWorld. Wolfram Research, Inc. Archived from the original on 2005-11-27. Retrieved 2015-11-06.
7. Weisstein, Eric Wolfgang. "Covercosine". MathWorld. Wolfram Research, Inc. Archived from the original on 2014-03-28. Retrieved 2015-11-06.