Closed-loop transfer function

A closed-loop transfer function in control theory is a mathematical expression (algorithm) describing the net result of the effects of a closed (feedback) loop on the input signal to the circuits enclosed by the loop.

Overview

The closed-loop transfer function is measured at the output. The output signal waveform can be calculated from the closed-loop transfer function and the input signal waveform.

An example of a closed-loop transfer function is shown below:

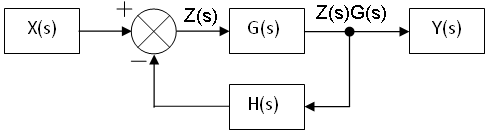
The summing node and the G(s) and H(s) blocks can all be combined into one block, which would have the following transfer function:

${\displaystyle {\dfrac {Y(s)}{X(s)}}={\dfrac {G(s)}{1+G(s)H(s)}}}$

${\displaystyle G(s)}$ is called feedforward transfer function, ${\displaystyle H(s)}$ is called feedback transfer function, and their product ${\displaystyle G(s)H(s)}$ is called the Open loop transfer function.

Derivation

We define an intermediate signal Z (also known as error signal) shown as follows:

Using this figure we write:

${\displaystyle Y(s)=G(s)Z(s)}$

${\displaystyle Z(s)=X(s)-H(s)Y(s)}$

Now, plug the second equation into the first to eliminate Z(s):

${\displaystyle Y(s)=G(s)[X(s)-H(s)Y(s)]}$

Move all the terms with Y(s) to the left hand side, and keep the term with X(s) on the right hand side:

${\displaystyle Y(s)+G(s)H(s)Y(s)=G(s)X(s)}$

Therefore,

${\displaystyle Y(s)(1+G(s)H(s))=G(s)X(s)}$

${\displaystyle \Rightarrow {\dfrac {Y(s)}{X(s)}}={\dfrac {G(s)}{1+G(s)H(s)}}}$

See also

• Federal Standard 1037C
• Open-loop controller
• Open-Loop Transfer Function

References

•  This article incorporates public domain material from the General Services Administration document: "Federal Standard 1037C".